搜索
【题目】已知
，函数
的最小值为1.
(1)求
的值；
(2)若
，求实数
的最大值.
参考答案：
【答案】（1）
（2）
【解析】【试题分析】（1）运用绝对值的三角不等式
或运用绝对值的定义将其化归为分段函数的最值问题来处理，求解时借助分段函数的单调性可知
在
上单调递减， 
在
上单调递增，从而探求出
在
处取最小值；（2）先将不等式中的参数
分离出来得到
，再运用基本不等式或柯西不等式求
最值：
（1）法一： 
，
∵
且
，
∴
，当
时取等号，即
的最小值为
，
∴
；
法二：∵
， ∴
，
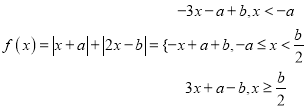显然
在
上单调递减， 
在
上单调递增，
∴
的最小值为
， ∴
；
（2）法一：∵
恒成立，∴
恒成立，
，
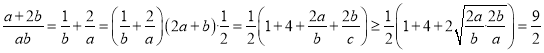当
时， 
取得最小值
， ∴
，即实数
的最大值为
；
法二：∵
恒成立， ∴
恒成立， 
恒成立， 
， ∴
，即实数
的最大值为
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
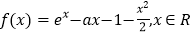
（Ⅰ）若
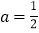，求函数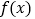
的单调区间；（Ⅱ）若对任意
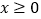都有
恒成立，求实数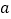
的取值范围；（Ⅲ）设函数
，求证：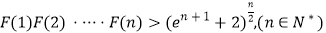
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一直线l过直线l1：3x﹣y=3和直线l2：x﹣2y=2的交点P，且与直线l3：x﹣y+1=0垂直．
（1）求直线l的方程；
（2）若直线l与圆心在x正半轴上的半径为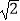
的圆C相切，求圆C的标准方程． -
科目： 来源： 题型：
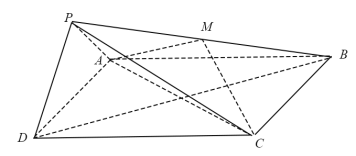
查看答案和解析>>【题目】如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD//平面MAC，PA=PD=
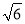，AB=4．（I）求证：M为PB的中点；
（II）求二面角B-PD-A的大小；
（III）求直线MC与平面BDP所成角的正弦值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在长方体ABCD﹣A1B1C1D1中，BC=2AB=4，
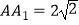，E是A1D1的中点．
（Ⅰ）在平面A1B1C1D1内，请作出过点E与CE垂直的直线l，并证明l⊥CE；
（Ⅱ）设（Ⅰ）中所作直线l与CE确定的平面为α，求点C1到平面α的距离．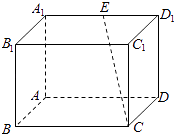
-
科目： 来源： 题型：
查看答案和解析>>【题目】设f（x）是定义在R上的奇函数，且当x≥0时，f（x）=x2 ， 若对任意的x∈[t，t+2]，不等式f（x+t）≥2f（x）恒成立，则实数t的取值范围是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
．（1）当
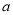为何值时，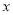 
轴为曲线
的切线；（2）用
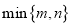表示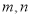
中的最小值，设函数
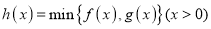，讨论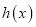
零点的个数．
相关试题
