【题目】已知函数f(x)=2 ![]() sin(
sin( ![]() +
+ ![]() )sin(
)sin( ![]() ﹣
﹣ ![]() )﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x=
)﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x= ![]() 对称.
对称.
(1)若存在x∈[0, ![]() ),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
(2)若当x∈[0, ![]() ]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
参考答案:
【答案】
(1)解:f(x)= ![]() sin(x+
sin(x+ ![]() )+sinx=
)+sinx= ![]() cosx+sinx=2sin(x+
cosx+sinx=2sin(x+ ![]() ).
).
函数y=g(x)的图象上取点(x,y),关于直线x= ![]() 对称点的坐标为(
对称点的坐标为( ![]() ﹣x,y),
﹣x,y),
代入f(x)=2sin(x+ ![]() ),可得y=2sin(
),可得y=2sin( ![]() ﹣x),
﹣x),
x∈[0, ![]() ),则
),则 ![]() ﹣x∈[
﹣x∈[ ![]() ,
, ![]() ],∴y∈[1,2],
],∴y∈[1,2],
等式[g(x)]2﹣mg(x)+2=0,可化为m=y+ ![]() ,
,
∴y= ![]() 时,m的最小值为2
时,m的最小值为2 ![]() ;m=1或2时,m的最大值为3
;m=1或2时,m的最大值为3
(2)解:当x∈[0, ![]() ]时,f(x)∈[﹣
]时,f(x)∈[﹣ ![]() ,1],g(﹣x)∈[﹣1,1],
,1],g(﹣x)∈[﹣1,1],
∵当x∈[0, ![]() ]时不等式f(x)+ag(﹣x)>0恒成立,
]时不等式f(x)+ag(﹣x)>0恒成立,
∴a ![]() 或a
或a ![]()
【解析】(1)先求出f(x),g(x)的解析式,确定g(x)∈[1,2],等式[g(x)]2﹣mg(x)+2=0,可化为m=y+ ![]() ,即可求实数m的最大值和最小值(2)当x∈[0,
,即可求实数m的最大值和最小值(2)当x∈[0, ![]() ]时,f(x)∈[﹣
]时,f(x)∈[﹣ ![]() ,1],g(﹣x)∈[﹣1,1],利用当x∈[0,
,1],g(﹣x)∈[﹣1,1],利用当x∈[0, ![]() ]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)是这样定义的:对于任意整数m,当实数x满足不等式|x﹣m|<
 时,有f(x)=m.
时,有f(x)=m.
(1)求函数f(x)的定义域D,并画出它在x∈D∩[0,3]上的图象;
(2)若数列an=2+10( )n , 记Sn=f(a1)+f(a2)+f(a3)+…+f(an),求Sn .
)n , 记Sn=f(a1)+f(a2)+f(a3)+…+f(an),求Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10
 米,记∠BHE=θ.
米,记∠BHE=θ. 
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)问:当θ取何值时,污水净化效果最好?并求出此时管道的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
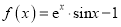 ,
,(Ⅰ)求曲线
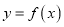 在点
在点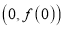 处的切线方程;
处的切线方程;(Ⅱ)求
 在区间
在区间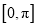 上零点个数.
上零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 是
是 上的减函数,
上的减函数, ,且 f [ f(x)]=16x-3.
,且 f [ f(x)]=16x-3.(1)求
 ;
;(2)若
 在(-2,3)单调递增,求实数
在(-2,3)单调递增,求实数 的取值范围;
的取值范围;(3)当
 时,
时, 有最大值1,求实数
有最大值1,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
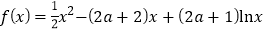 .
.(1)求
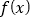 的单调区间;
的单调区间;(2)对任意的
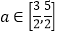 ,
, 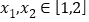 ,恒有
,恒有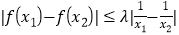 ,求正实数
,求正实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】几位同学在研究函数

 时,给出了下面几个结论:
时,给出了下面几个结论:①
 的单调减区间是
的单调减区间是 ,单调增区间是
,单调增区间是 ;
;②若
 ,则一定有
,则一定有 ;
; ③函数
 的值域为
的值域为 ;
;④若规定
 ,
, ,则
,则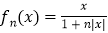 对任意
对任意 恒成立.
恒成立.上述结论中正确的是____
相关试题

