【题目】如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10 ![]() 米,记∠BHE=θ.
米,记∠BHE=θ. 
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)问:当θ取何值时,污水净化效果最好?并求出此时管道的长度.
参考答案:
【答案】
(1)解:由题意可得EH= ![]() ,FH=
,FH= ![]() ,EF=
,EF= ![]() ,由于 BE=10tanθ≤10
,由于 BE=10tanθ≤10 ![]() ,AF=
,AF= ![]() ≤10
≤10 ![]() ,
,
而且 ![]() ≤tanθ≤
≤tanθ≤ ![]() ,θ∈[
,θ∈[ ![]() ,
, ![]() ],
],
∴L= ![]() +
+ ![]() +
+ ![]() ,θ∈[
,θ∈[ ![]() ,
, ![]() ].
].
即L=10× ![]() ,θ∈[
,θ∈[ ![]() ,
, ![]() ]
]
(2)解:设sinθ+cosθ=t,则 sinθcosθ= ![]() ,由于θ∈[
,由于θ∈[ ![]() ,
, ![]() ],∴sinθ+cosθ=t=
],∴sinθ+cosθ=t= ![]() sin(θ+
sin(θ+ ![]() )∈[
)∈[ ![]() ,
, ![]() ].
].
由于L= ![]() 在[
在[ ![]() ,
, ![]() ]上是单调减函数,∴当t=
]上是单调减函数,∴当t= ![]() 时,即 θ=
时,即 θ= ![]() 或θ=
或θ= ![]() 时,L取得最大值为 20(
时,L取得最大值为 20( ![]() +1)米
+1)米
【解析】(1)解直角三角形求得得EH、FH、EF的解析式,再由 L=EH+FH+EF得到污水净化管道的长度L的函数解析式,并注明θ的范围.(2)设sinθ+cosθ=t,根据函数 L= ![]() 在[
在[ ![]() ,
, ![]() ]上是单调减函数,可求得L的最大值.
]上是单调减函数,可求得L的最大值.
【考点精析】认真审题,首先需要了解三角函数的最值(函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1∶3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文、理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如图所示.

(1)求a的值,并计算所抽取样本的平均值
 (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);(2)填写下面的2×2列联表,并判断能否有超过95%的把握认为“获奖与学生的文、理科有关”?
文科生
理科生
合计
获奖
5
不获奖
合计
200
附表及公式:

P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左右焦点分别为
的左右焦点分别为 ,上顶点为
,上顶点为 ,若直线
,若直线 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为 ,
,  的周长为
的周长为 .
.(1)求椭圆的标准方程;
(2)过点
 的直线
的直线 (直线
(直线 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于 两点,点
两点,点 在点
在点 的上方,若
的上方,若 ,求直线
,求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)是这样定义的:对于任意整数m,当实数x满足不等式|x﹣m|<
 时,有f(x)=m.
时,有f(x)=m.
(1)求函数f(x)的定义域D,并画出它在x∈D∩[0,3]上的图象;
(2)若数列an=2+10( )n , 记Sn=f(a1)+f(a2)+f(a3)+…+f(an),求Sn .
)n , 记Sn=f(a1)+f(a2)+f(a3)+…+f(an),求Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
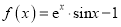 ,
,(Ⅰ)求曲线
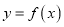 在点
在点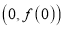 处的切线方程;
处的切线方程;(Ⅱ)求
 在区间
在区间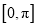 上零点个数.
上零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2
 sin(
sin(  +
+  )sin(
)sin(  ﹣
﹣  )﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x=
)﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x=  对称.
对称.
(1)若存在x∈[0, ),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
(2)若当x∈[0, ]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 是
是 上的减函数,
上的减函数, ,且 f [ f(x)]=16x-3.
,且 f [ f(x)]=16x-3.(1)求
 ;
;(2)若
 在(-2,3)单调递增,求实数
在(-2,3)单调递增,求实数 的取值范围;
的取值范围;(3)当
 时,
时, 有最大值1,求实数
有最大值1,求实数 的值.
的值.
相关试题

