【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)对任意的![]() ,
, ![]() ,恒有
,恒有![]() ,求正实数
,求正实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析(2)![]() .
.
【解析】试题分析:(1)先确定函数的定义域然后求导数fˊ(x),再对字母a分类讨论,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,求出单调区间.
(2)根据第一问的单调性,知f(x)在[1,2]上为减函数.若x1=x2,则原不等式恒成立;若x1≠x2,不妨设1≤x1<x2≤2,则f(x1)>f(x2),![]() ,所以原不等式进行化简整理得
,所以原不等式进行化简整理得![]() 对任意的
对任意的![]() 恒成立,令
恒成立,令![]() ,转化成研究g(x)在[1,2]的单调性,再利用导数即可求出正实数λ的取值范围.
,转化成研究g(x)在[1,2]的单调性,再利用导数即可求出正实数λ的取值范围.
试题解析:
(1)![]() =
=![]() ,
,
令f'(x)=0,则x1=2a+1,x2=1.
①当a=0时,![]() ,所以f(x)增区间是(0,+∞);
,所以f(x)增区间是(0,+∞);
②当a>0时,2a+1>1,
所以f(x)增区间是(0,1)与(2a+1,+∞),减区间是(1,2a+1);
③当![]() 时,0<2a+1<1,
时,0<2a+1<1,
所以f(x)增区间是(0,2a+1)与(1,+∞),减区间是(2a+1,1);
④当![]() 时,2a+1≤0,
时,2a+1≤0,
所以f(x)增区间是(1,+∞),减区间是(0,1).
(2)因为![]() ,所以(2a+1)∈[4,6],
,所以(2a+1)∈[4,6],
由(1)知f(x)在[1,2]上为减函数.
若x1=x2,则原不等式恒成立,∴λ∈(0,+∞).
若x1≠x2,不妨设1≤x1<x2≤2,则f(x1)>f(x2),![]() ,
,
所以原不等式即为:![]() ,
,
即![]() 对任意的
对任意的![]() ,x1,x2∈[1,2]恒成立.
,x1,x2∈[1,2]恒成立.
令![]() ,
,
所以对任意的![]() ,x1,x2∈[1,2]有g(x1)<g(x2)恒成立,
,x1,x2∈[1,2]有g(x1)<g(x2)恒成立,
所以![]() 在闭区间[1,2]上为增函数.
在闭区间[1,2]上为增函数.
所以g'(x)≥0对任意的![]() ,x∈[1,2]恒成立.
,x∈[1,2]恒成立.
而![]() ,g'(x)=x﹣(2a+2)
,g'(x)=x﹣(2a+2)![]() ,化简即x3﹣(2a+2)x2+(2a+1)x+λ≥0,
,化简即x3﹣(2a+2)x2+(2a+1)x+λ≥0,
即(2x﹣2x2)a+x3﹣2x2+x+λ≥0,其中![]() .
.
∵x∈[1,2],∴2x﹣2x2≤0,∴只需![]() .
.
即x3﹣7x2+6x+λ≥0对任意x∈[1,2]恒成立.
令h(x)=x3﹣7x2+6x+λ,x∈[1,2],h'(x)=3x2﹣14x+6<0恒成立.
∴h(x)=x3﹣7x2+6x+λ在闭区间[1,2]上为减函数,则hmin(x)=h(2)=λ﹣8,
∴hmin(x)=h(2)=λ﹣8≥0,解得λ≥8.
故正实数λ的取值范围[8,+∞)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
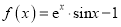 ,
,(Ⅰ)求曲线
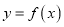 在点
在点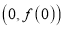 处的切线方程;
处的切线方程;(Ⅱ)求
 在区间
在区间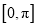 上零点个数.
上零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2
 sin(
sin(  +
+  )sin(
)sin(  ﹣
﹣  )﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x=
)﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x=  对称.
对称.
(1)若存在x∈[0, ),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
(2)若当x∈[0, ]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 是
是 上的减函数,
上的减函数, ,且 f [ f(x)]=16x-3.
,且 f [ f(x)]=16x-3.(1)求
 ;
;(2)若
 在(-2,3)单调递增,求实数
在(-2,3)单调递增,求实数 的取值范围;
的取值范围;(3)当
 时,
时, 有最大值1,求实数
有最大值1,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】几位同学在研究函数

 时,给出了下面几个结论:
时,给出了下面几个结论:①
 的单调减区间是
的单调减区间是 ,单调增区间是
,单调增区间是 ;
;②若
 ,则一定有
,则一定有 ;
; ③函数
 的值域为
的值域为 ;
;④若规定
 ,
, ,则
,则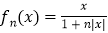 对任意
对任意 恒成立.
恒成立.上述结论中正确的是____
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , 若对任意的正整数n,总存在正整数m,使得Sn=am , 则称{an}是“H数列”.
(1)若数列{an}的前n项和为Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0,若{an}是“H数列”,求d的值;
(3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知函数f(x)=

(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
相关试题

