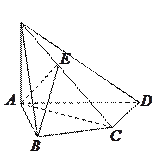
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)证明![]() ;
;
(Ⅱ)证明![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
参考答案:
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意可得CD⊥平面PAC,结合线面垂直的定义即可得到AE⊥CD;
(Ⅱ)由题意可得AE⊥PD,AB⊥PD.利用线面垂直的判断定理可得证明![]() 平面
平面![]() ;
;
(Ⅲ)由题意找到二面角的平面角,结合三角形的边长关系可得二面角![]() 的大小是
的大小是![]() .
.
试题解析:
(I)证明:在四棱锥PABCD中,
因PA⊥底面ABCD,CD平面ABCD,故PA⊥CD.
∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
而AE平面PAC,
∴AE⊥CD.
(II)证明:由PA=AB=BC,∠ABC=60,可得AC=PA.
∵E是PC的中点,∴AE⊥PC.
由(I)知,AE⊥CD,且PC∩CD=C,所以AE⊥平面PCD.
而PD平面PCD,∴AE⊥PD.
∵PA⊥底面ABCD,PD在底面ABCD内射影是AD,AB⊥AD,∴AB⊥PD.
又AB∩AE=A,综上得PD⊥平面ABE.
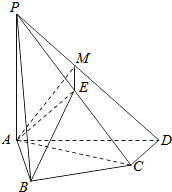
(III)过点A作AM⊥PD,垂足为M,连接EM.
由(II)知,AE⊥平面PCD,AM在平面PCD内的射影是EM,则EM⊥PD.
因此∠AME是二面角APDC的平面角。
由已知,得∠CAD=30°.设AC=a,可得![]() .
.
在Rt△ADP中,∵AM⊥PD,∴AM.PD=PA.AD.则![]() .
.
在Rt△AEM中, ![]() .
.
所以二面角APDC的大小是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:x∈(﹣∞,0),2x<3x;命题q:x∈(0,
 ),tanx>sinx,则下列命题为真命题的是( )
),tanx>sinx,则下列命题为真命题的是( )
A.p∧q
B.p∨(﹁q)
C.(﹁p)∧q
D.p∧(﹁q) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U=R,集合A={x|x<﹣4,或x>2},B={x|﹣1≤2x﹣1﹣2≤6}.
(1)求A∩B、(UA)∪(UB);
(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x2﹣4x+3|,x∈R.
(1)在区间[0,4]上画出函数f(x)的图象;
(2)写出该函数在R上的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=a+
 为定义在R上的奇函数.
为定义在R上的奇函数.
(1)求a的值;
(2)判断函数f(x)在(﹣∞,+∞)的单调性并给予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】理科竞赛小组有9名女生、12名男生,从中随机抽取一个容量为7的样本进行分析.
(Ⅰ)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可)
(Ⅱ)如果随机抽取的7名同学的物理、化学成绩(单位:分)对应如表:
学生序号
1
2
3
4
5
6
7
物理成绩
65
70
75
81
85
87
93
化学成绩
72
68
80
85
90
86
91
规定85分以上(包括85份)为优秀,从这7名同学中再抽取3名同学,记这3名同学中物理和化学成绩均为优秀的人数为X,求随机变量X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数x,y满足ax<ay(0<a<1),则下列关系式恒成立的是( )
A.x3>y3
B.sinx>siny
C.ln(x2+1)>ln(y2+1)
D.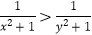
相关试题

