【题目】函数f(x)=a+ ![]() 为定义在R上的奇函数.
为定义在R上的奇函数.
(1)求a的值;
(2)判断函数f(x)在(﹣∞,+∞)的单调性并给予证明.
参考答案:
【答案】
(1)
解:∵函数 ![]() 为定义在R上的奇函数.
为定义在R上的奇函数.
∴f(0)=0,
即 ![]() ,解得
,解得 ![]()
(2)
解:由(1)知 ![]() ,则
,则 ![]() ,
,
函数f(x)在(﹣∞,+∞)上单调递减,给出如下证明:
证法一:任取x1,x2∈(﹣∞,+∞),且x1<x2,
则 ![]()
= ![]() =
= ![]() )
)
= ![]() ,
,
∵x1<x2,∴x2﹣x1>0,∴ ![]() ,∴
,∴ ![]() ,
,
又∵ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() >0,即f(x2)﹣f(x1)>0,
>0,即f(x2)﹣f(x1)>0,
∴f(x2)>f(x1),
∴函数f(x)在(﹣∞,+∞)上单调递减.
证法二:∵ ![]()
∴ ![]() ,
,
∵f′(x)<0恒成立,
故函数f(x)在(﹣∞,+∞)上单调递减.
【解析】(1)函数 ![]() 为定义在R上的奇函数.则f(0)=0,解得a的值;(2)证法一:任取x1 , x2∈(﹣∞,+∞),且x1<x2 , 作差判断f(x2)与f(x1)的大小,结合单调性的定义,可得函数f(x)在(﹣∞,+∞)的单调性;
为定义在R上的奇函数.则f(0)=0,解得a的值;(2)证法一:任取x1 , x2∈(﹣∞,+∞),且x1<x2 , 作差判断f(x2)与f(x1)的大小,结合单调性的定义,可得函数f(x)在(﹣∞,+∞)的单调性;
证法二:求导,判断导函数的符号,进而可得函数f(x)在(﹣∞,+∞)的单调性.
【考点精析】本题主要考查了函数单调性的判断方法和函数奇偶性的性质的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U=R,集合A={x|x<﹣4,或x>2},B={x|﹣1≤2x﹣1﹣2≤6}.
(1)求A∩B、(UA)∪(UB);
(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x2﹣4x+3|,x∈R.
(1)在区间[0,4]上画出函数f(x)的图象;
(2)写出该函数在R上的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
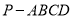 中,
中, 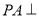 底面
底面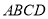 ,
, 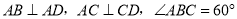 ,
, 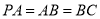 ,
, 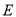 是
是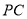 的中点.
的中点.(Ⅰ)证明
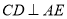 ;
;(Ⅱ)证明
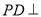 平面
平面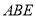 ;
;(Ⅲ)求二面角
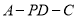 的大小.
的大小.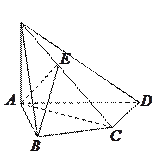
-
科目: 来源: 题型:
查看答案和解析>>【题目】理科竞赛小组有9名女生、12名男生,从中随机抽取一个容量为7的样本进行分析.
(Ⅰ)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可)
(Ⅱ)如果随机抽取的7名同学的物理、化学成绩(单位:分)对应如表:
学生序号
1
2
3
4
5
6
7
物理成绩
65
70
75
81
85
87
93
化学成绩
72
68
80
85
90
86
91
规定85分以上(包括85份)为优秀,从这7名同学中再抽取3名同学,记这3名同学中物理和化学成绩均为优秀的人数为X,求随机变量X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数x,y满足ax<ay(0<a<1),则下列关系式恒成立的是( )
A.x3>y3
B.sinx>siny
C.ln(x2+1)>ln(y2+1)
D.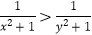
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A=[0,
 ),B=[
),B=[ , 1],函数f (x)=
, 1],函数f (x)= , 若x0∈A,且f[f (x0)]∈A,则x0的取值范围是( )
, 若x0∈A,且f[f (x0)]∈A,则x0的取值范围是( )
A.(0, ]
]
B.[ ,
,  ]
]
C.( ,
,  )
)
D.[0, ]
]
相关试题

