【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD= ![]() BC,
BC, ![]() =
= ![]()
![]() .
. 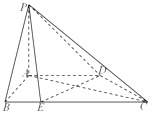
(1)求证:DE⊥平面PAC;
(2)若直线PE与平面PAC所成角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.
参考答案:
【答案】
(1)证明:以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
设AB=AD= ![]() BC=2,
BC=2,
则D(0,2,0),E(2,1,0),A(0,0,0),C(2,4,0),
![]() =(2,﹣1,0),
=(2,﹣1,0), ![]() =(2,4,0),
=(2,4,0),
![]() =4﹣4+0=0,∴DE⊥AC,
=4﹣4+0=0,∴DE⊥AC,
∵PA⊥平面ABCD,DE平面ABCD,∴DE⊥PA,
∵PA∩AC=A,∴DE⊥平面PAC
(2)解:设P(0,0,t),(t>0), ![]() =(0,0,t),
=(0,0,t), ![]() =(2,4,0),
=(2,4,0), ![]() =(2,1,﹣t),
=(2,1,﹣t),
设平面PAC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 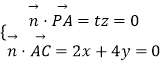 ,取x=2,得
,取x=2,得 ![]() =(2,﹣1,0),
=(2,﹣1,0),
∵直线PE与平面PAC所成角的正弦值为 ![]() ,
,
∴ 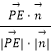 =
= ![]() =
= ![]() ,解得t=1,或t=﹣1(舍),
,解得t=1,或t=﹣1(舍),
∴P(0,0,1), ![]() =(2,4,﹣1),
=(2,4,﹣1), ![]() =(0,2,﹣1),
=(0,2,﹣1),
设平面PCD的法向量 ![]() =(a,b,c),
=(a,b,c),
则 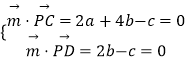 ,取b=1,得
,取b=1,得 ![]() =(﹣1,1,2),
=(﹣1,1,2),
设二面角A﹣PC﹣D的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
二面角A﹣PC﹣D的平面角的余弦值为 ![]() .
.
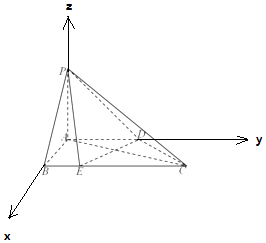
【解析】(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能证明DE⊥平面PAC.(2)求出平面PAC的法向量和平面PCD的法向量,利用向量法能求出二面角A﹣PC﹣D的平面角的余弦值.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
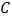 :
:  过点
过点 的直线交抛物线
的直线交抛物线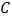 于
于 两点,设
两点,设
(1)若点
 关于
关于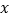 轴的对称点为
轴的对称点为 ,求证:直线
,求证:直线 经过抛物线
经过抛物线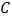 的焦点
的焦点 ;
;(2)若
 求当
求当 最大时,直线
最大时,直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)g(x)分别是定义在R上的偶函数和奇函数,且f(x)+g(x)=23x.
(1)证明:f(x)-g(x)=23-x,并求函数f(x),g(x)的解析式;
(2)解关于x不等式:g(x2+2x)+g(x-4)>0;
(3)若对任意x∈R,不等式f(2x)≥mf(x)-4恒成立,求实数m的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
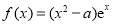 ,
, .
.(Ⅰ)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)若在区间
 上存在不相等的实数
上存在不相等的实数 ,使
,使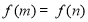 成立,求
成立,求 的取值范围;
的取值范围;(Ⅲ)若函数
 有两个不同的极值点
有两个不同的极值点 ,
, ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
.(1)求
 的值;
的值;(2)求
 在
在 上的单调区间;
上的单调区间;(3)求
 在
在 上的最大值.
上的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100﹣110的学生数有21人
(1)求总人数N和分数在110﹣115分的人数n.;
(2)现准备从分数在110﹣115的n名学生(女生占 )中选3位分配给A老师进行指导,设随机变量ξ表示选出的3位学生中女生的人数,求ξ的分布列与数学期望Eξ;
)中选3位分配给A老师进行指导,设随机变量ξ表示选出的3位学生中女生的人数,求ξ的分布列与数学期望Eξ;
(3)为了分析某个学生的学习状态,对其下一阶段的学习提供指导建议,对他前7次考试的数学成绩x、物理成绩y进行分析,该生7次考试成绩如表数学(x)
88
83
117
92
108
100
112
物理(y)
94
91
108
96
104
101
106
已知该生的物理成绩y与数学成绩x是线性相关的,求出y关于x的线性回归方程
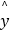 =
= 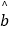 x+
x+ 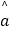 .若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
.若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据(x1 , y1),(x2 , y2),…,(xn , yn),其回归方程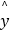 =
= 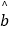 x+
x+ 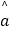 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 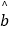 =
= 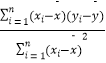 ,
, 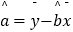 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆N:x2+(y+
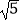 )2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,
)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0, 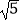 )和DP上的点M,满足
)和DP上的点M,满足 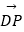 =2
=2 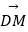 ,
, 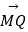
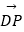 =0.
=0. 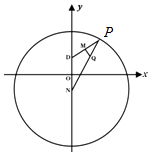
(1)当P在圆上运动时,求点Q的轨迹方程;
(2)若斜率为 的直线l与(1)中所求Q的轨迹交于不同两点A、B,又点C(
的直线l与(1)中所求Q的轨迹交于不同两点A、B,又点C(  ,2),求△ABC面积最大值时对应的直线l的方程.
,2),求△ABC面积最大值时对应的直线l的方程.
相关试题

