【题目】已知抛物线![]() :
: ![]() 过点
过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,设
两点,设![]()
(1)若点 ![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求证:直线
,求证:直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ;
;
(2)若![]() 求当
求当![]() 最大时,直线
最大时,直线![]() 的方程.
的方程.
参考答案:
【答案】(1)证明见解析.
(2)![]() .
.
【解析】试题分析:(1)设出P和Q的坐标,根据P和M关于x轴对称表示出M的坐标,利用设出的坐标表示出![]() 和
和![]() ,根据
,根据![]() ,化简即可得到P和Q的横坐标,然后由抛物线的方程找出焦点F的坐标,然后利用M,F和Q的坐标表示出向量
,化简即可得到P和Q的横坐标,然后由抛物线的方程找出焦点F的坐标,然后利用M,F和Q的坐标表示出向量![]() ,利用刚才化简的式子及求出的横坐标代入即可得到
,利用刚才化简的式子及求出的横坐标代入即可得到![]() =λ
=λ![]() ,所以得到直线MQ过F点;(2)由第一问求得的P和Q的横坐标相乘等于1,由y12﹣y22=16x1x2=16,y1y2>0,得到y1y2的值,利用两点间的距离公式表示出|PQ|2,然后把P和Q的横坐标及得到的y1y2的值及x1x2的值分别代入得到关于λ的关系式,配方后利用λ的范围求出λ+
,所以得到直线MQ过F点;(2)由第一问求得的P和Q的横坐标相乘等于1,由y12﹣y22=16x1x2=16,y1y2>0,得到y1y2的值,利用两点间的距离公式表示出|PQ|2,然后把P和Q的横坐标及得到的y1y2的值及x1x2的值分别代入得到关于λ的关系式,配方后利用λ的范围求出λ+![]() 的范围,即可求出λ+
的范围,即可求出λ+![]() 的最大值,让其等于最大值解出此时λ的值,把λ的值代入关于λ的关系式即可求出|PQ|2的最大值,即得到|PQ|最大值,并利用λ的值求出此时P和Q两点的坐标,根据两点的坐标即可写出直线PQ的方程.
的最大值,让其等于最大值解出此时λ的值,把λ的值代入关于λ的关系式即可求出|PQ|2的最大值,即得到|PQ|最大值,并利用λ的值求出此时P和Q两点的坐标,根据两点的坐标即可写出直线PQ的方程.
详解:
(1)设![]()
![]()
![]()
![]()
![]()
![]()
由抛物线C:![]() 得到F(1,0)
得到F(1,0)
![]()
![]() 直线MQ经过抛物线C的焦点F;
直线MQ经过抛物线C的焦点F;
(2)由(1)知![]()
则![]()
![]()
![]()
当 ![]() 即
即 ![]() 时,
时, ![]() 有最大值
有最大值![]() ,则
,则![]() 的最大值为
的最大值为![]()
此时![]()
![]() 则直线的方程为:
则直线的方程为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的内角A、B、C的对边分别为a、b、c,且3bcos A=ccos A+acosC.
(1)求tanA的值;
(2)若a=4 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是最近十届奥运会的年份、届别、主办国,以及主办国在上届获得的金牌数、当届
获得的金牌数的统计数据:
年份
1972
1976
1980
1984
1988
1992
1996
2000
2004
2008
届别
20
21
22
23
24
25
26
27
28
29
主办国家
联邦
德国
加拿大
苏联
美国
韩国
西班牙
美国
澳大
利亚
希腊
中国
上届金牌数
5
0
49
未参加
6
1
37
9
4
32
当界金牌数
13
0
80
83
12
13
44
16
6
51
某体育爱好组织,利用上表研究所获金牌数与主办奥运会之间的关系,
(1)求出主办国在上届所获金牌数(设为
 )与在当届所获金牌数(设为
)与在当届所获金牌数(设为 )之间的线性回归方程
)之间的线性回归方程 其中
其中
(2)在2008年第29届北京奥运会上日本获得9块金牌,则据此线性回归方程估计在2020 年第 32 届东
京奥运会上日本将获得的金牌数为(所有金牌数精确到整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=logax(a>1)在[a,2a]上的最大值是最小值的2倍.
(1)若函数g(x)=f(3x2-mx+5)在区间[-1,+∞)上是增函数,求实数m的取值范围;
(2)设函数F(x)=f(
 )(2x),且关于x的方程F(x)=k在[
)(2x),且关于x的方程F(x)=k在[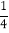 ,4]上有解,求实数k的取值范围.
,4]上有解,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)g(x)分别是定义在R上的偶函数和奇函数,且f(x)+g(x)=23x.
(1)证明:f(x)-g(x)=23-x,并求函数f(x),g(x)的解析式;
(2)解关于x不等式:g(x2+2x)+g(x-4)>0;
(3)若对任意x∈R,不等式f(2x)≥mf(x)-4恒成立,求实数m的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
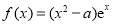 ,
, .
.(Ⅰ)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)若在区间
 上存在不相等的实数
上存在不相等的实数 ,使
,使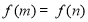 成立,求
成立,求 的取值范围;
的取值范围;(Ⅲ)若函数
 有两个不同的极值点
有两个不同的极值点 ,
, ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD=
 BC,
BC, 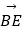 =
= 
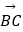 .
. 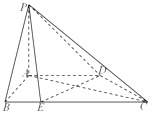
(1)求证:DE⊥平面PAC;
(2)若直线PE与平面PAC所成角的正弦值为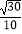 ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.
相关试题

