【题目】种子发芽率与昼夜温差有关.某研究性学习小组对此进行研究,他们分别记录了3月12日至3月16日的昼夜温差与每天100颗某种种子浸泡后的发芽数,如下表:

(I)从3月12日至3月16日中任选2天,记发芽的种子数分别为c,d,求事件“c,d均不小于25”的概率;
(II)请根据3月13日至3月15日的三组数据,求出y关于x的线性回归方程![]() ;
;
(III)若由线性回归方程得到的估计数据与实际数据误差均不超过2颗,则认为回归方程是可靠的,试用3月12日与16日的两组数据检验,(II)中的回归方程是否可靠?
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)详见解析.
;(3)详见解析.
【解析】试题分析:(1)由列举法得出从5天中任选2天的基本事件, 选出的二天种子发芽数均不小于25的基本事件,根据古典概型得出概率;(2)先求出平均数和![]() 代入公式,求出线性回归方程;(3)将
代入公式,求出线性回归方程;(3)将![]() 和
和![]() 代入方程,与(II)中的回归方程进行比较,得出结论.
代入方程,与(II)中的回归方程进行比较,得出结论.
试题解析:(Ⅰ)从5天中任选2天,共有10个基本事件:(12日,13日),(12日,14日),(12日,15日),
(12日,16日),(13日,14日),(13日,15日),(13日,16日),(14日,15日),(14日,16日),(15日,16日).
选出的二天种子发芽数均不小于25共有3个基本事件:(13日,14日),(13日,15日),(14日,15日).
∴事件“![]() 均不小于25”的概率为
均不小于25”的概率为![]() .
.
(Ⅱ)![]() .
. ![]() 5.
5. ![]() =2.
=2.
∴![]() .
.
∴![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(Ⅲ)当![]() 时,
时, ![]() .
.
当![]() 时,
时, ![]() .
.
∴回归方程![]() 是可靠的.
是可靠的.
点睛:具有以下两个特点的概率模型称为古典概率模型,简称古典概型:(1)试验中所有可能出现的基本事件只有有限个.(2)每个基本事件出现的可能性相等.如果一次试验中可能出现的结果有n个,而且所有结果出现的可能性都相等,那么每一个基本事件的概率都是![]() ;如果某个事件A包括的结果有m个,那么事件A的概率P(A)=
;如果某个事件A包括的结果有m个,那么事件A的概率P(A)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号
第一组
第二组
第三组
第四组
第五组
分组
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
(Ⅰ)求图中a的值;
(Ⅱ)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(Ⅲ)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:若实数x满足x2﹣4ax+3a2≤0,其中a>0;命题q:实数x满足

(1)若a=1且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围. -
科目: 来源: 题型:
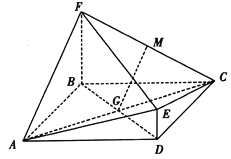
查看答案和解析>>【题目】如图,菱
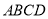 与四边形BDEF相交于BD,
与四边形BDEF相交于BD, 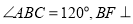 平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点,
平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点, 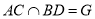 .
.(I)求证:GM//平面CDE;
(II)求证:平面ACE⊥平面ACF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 的定义域为( )
的定义域为( )
A.{x|x≥1}
B.{x|x≥1或x=0}
C.{x|x≥0}
D.{x|x=0} -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=4,且sinB,sinA,sinC成等差数列,建立适当的直角坐标系,求点A的轨迹方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a满足x+lgx=4,b满足x+10x=4,函数f(x)=
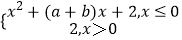 ,则关于x的方程f(x)=x的解的个数是( )
,则关于x的方程f(x)=x的解的个数是( )
A.1
B.2
C.3
D.4
相关试题

