【题目】在△ABC中,BC=4,且sinB,sinA,sinC成等差数列,建立适当的直角坐标系,求点A的轨迹方程.
参考答案:
【答案】解:以BC边所在直线为x轴,线段BC的垂直平分线为y轴,距离直角坐标系.则B(﹣2,0),C(2,0).∵BC=4,且sinB,sinA,sinC成等差数列,
∴2sinA=sinB+sinC,
由正弦定理可得:AC+AB=2BC=8>BC=4,
∴点A的轨迹是以B,C为焦点,8为实轴长的椭圆,除去椭圆与x轴的两个交点.
设要求的椭圆标准方程为 ![]() ,
,
∵c=2,a=4,∴b2=a2﹣c2=12.
∴椭圆的方程为: ![]()
【解析】以BC边所在直线为x轴,线段BC的垂直平分线为y轴,距离直角坐标系.则B(﹣2,0),C(2,0).由于BC=4,且sinB,sinA,sinC成等差数列,可得2sinA=sinB+sinC,由正弦定理可得:AC+AB=2BC=8>BC=4,可得点A的轨迹是以B,C为焦点,8为实轴长的椭圆,除去椭圆与x轴的两个交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱
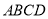 与四边形BDEF相交于BD,
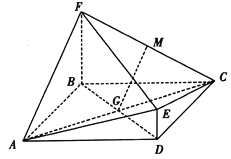
与四边形BDEF相交于BD, 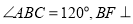 平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点,
平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点, 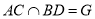 .
.(I)求证:GM//平面CDE;
(II)求证:平面ACE⊥平面ACF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】种子发芽率与昼夜温差有关.某研究性学习小组对此进行研究,他们分别记录了3月12日至3月16日的昼夜温差与每天100颗某种种子浸泡后的发芽数,如下表:

(I)从3月12日至3月16日中任选2天,记发芽的种子数分别为c,d,求事件“c,d均不小于25”的概率;
(II)请根据3月13日至3月15日的三组数据,求出y关于x的线性回归方程
 ;
;(III)若由线性回归方程得到的估计数据与实际数据误差均不超过2颗,则认为回归方程是可靠的,试用3月12日与16日的两组数据检验,(II)中的回归方程是否可靠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 的定义域为( )
的定义域为( )
A.{x|x≥1}
B.{x|x≥1或x=0}
C.{x|x≥0}
D.{x|x=0} -
科目: 来源: 题型:
查看答案和解析>>【题目】若a满足x+lgx=4,b满足x+10x=4,函数f(x)=
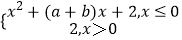 ,则关于x的方程f(x)=x的解的个数是( )
,则关于x的方程f(x)=x的解的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位学生参加数学竞赛培训,他们在培训期间8次模拟考试的成绩如下: 甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,并求学生乙成绩的平均数和方差;
(2)从甲同学超过80分的6个成绩中任取两个,求这两个成绩中至少有一个超过90分的概率.
(3)甲同学超过80(分)的成绩有82 81 95 88 93 84, -
科目: 来源: 题型:
查看答案和解析>>【题目】若两集合A=[0,3],B=[0,3],分别从集合A、B中各任取一个元素m、n,即满足m∈A,n∈B,记为(m,n), (Ⅰ)若m∈Z,n∈Z,写出所有的(m,n)的取值情况,并求事件“方程
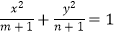 所对应的曲线表示焦点在x轴上的椭圆”的概率;
所对应的曲线表示焦点在x轴上的椭圆”的概率;
(Ⅱ)求事件“方程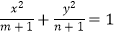 所对应的曲线表示焦点在x轴上的椭圆,且长轴长大于短轴长的
所对应的曲线表示焦点在x轴上的椭圆,且长轴长大于短轴长的 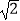 倍”的概率.
倍”的概率.
相关试题

