【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() .
.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)利用 ,化简得
,化简得![]() ,故
,故![]() 是等比数列;(2)由于
是等比数列;(2)由于![]() ,相等于一个等差数列乘以一个等比数列,所以考虑用错位相减求和法求前
,相等于一个等差数列乘以一个等比数列,所以考虑用错位相减求和法求前![]() 项和为
项和为![]() .
.
试题解析:
(1)当![]() 时,
时, ![]() ,解得
,解得![]() ;...............1分
;...............1分
当![]() 时,
时, ![]() ,两式相减得
,两式相减得![]() ,................3分
,................3分
化简得![]() ,所以数列
,所以数列![]() 是首项为1,公比为-1的等比数列..........5分
是首项为1,公比为-1的等比数列..........5分
(2)由(1)可得![]() ,所以
,所以![]() ,下提供三种求和方法供参考:.......6分
,下提供三种求和方法供参考:.......6分
【错位相减法】![]() ,
,
![]() ....................8分
....................8分
两式相减得![]() ................9分
................9分
 ....................10分
....................10分
![]() ,....................11分
,....................11分
所以数列![]() 的前
的前![]() 项和
项和![]() .........................12分
.........................12分
【并项求和法】
当![]() 为偶数时,
为偶数时, ![]() ;........................9分
;........................9分
当![]() 为奇数时,
为奇数时, ![]() 为偶数,
为偶数, ![]() ;............11分
;............11分
综上,数列![]() 的前
的前![]() 项和
项和![]() .........................12分
.........................12分
【裂项相消法】
因为![]() ..............9分
..............9分
所以![]()
![]() ,
,
所以数列![]() 的前
的前![]() 项和
项和![]() ..................12分
..................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】若对于定义在
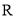 上的连续函数
上的连续函数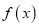 ,存在常数
,存在常数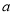 (
(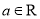 ),使得
),使得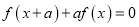 对任意的实数
对任意的实数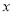 成立,则称
成立,则称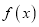 是回旋函数,且阶数为
是回旋函数,且阶数为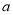 .
.(1)试判断函数
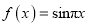 是否是一个阶数为1的回旋函数,并说明理由;
是否是一个阶数为1的回旋函数,并说明理由;(2)已知
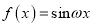 是回旋函数,求实数
是回旋函数,求实数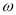 的值;
的值;(3)若回旋函数
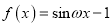 (
(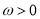 )在
)在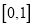 恰有100个零点,求实数
恰有100个零点,求实数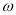 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
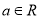 ,函数
,函数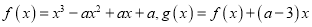 .
.(1)求证:曲线
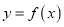 在点
在点 处的切线过定点;
处的切线过定点;(2)若
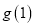 是
是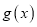 在区间
在区间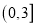 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数 的取值范围;
的取值范围;(3)求证:对任意给定的正数
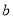 ,总存在
,总存在 ,使得
,使得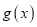 在
在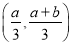 上为单调函数.
上为单调函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 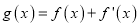
(Ⅰ)求
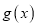 的单调区间和最小值;
的单调区间和最小值;(Ⅱ)讨论
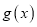 与
与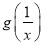 的大小关系;
的大小关系;(Ⅲ)求
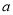 的取值范围,使得
的取值范围,使得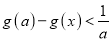 对任意
对任意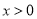 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面几种推理是合情推理的是 ( )
①由圆的性质类比出球的有关性质
②由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180°
③某次考试张军成绩是100分,由此推出全班同学成绩都是100分
④数列1,0,1,0,…,推测出每项公式
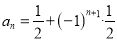
A. ①② B. ①③④ C. ①②④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的年销售量
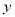 与该年广告费用支出
与该年广告费用支出 有关,现收集了4组观测数据列于下表:
有关,现收集了4组观测数据列于下表: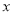 (万元)
(万元)1
4
5
6
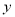 (万元)
(万元)30
40
60
50
现确定以广告费用支出
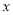 为解释变量,销售量
为解释变量,销售量 为预报变量对这两个变量进行统计分析.
为预报变量对这两个变量进行统计分析.(1)已知这两个变量满足线性相关关系,试建立
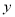 与
与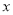 之间的回归方程;
之间的回归方程;(2)假如2017年广告费用支出为10万元,请根据你得到的模型,预测该年的销售量
 .
.(线性回归方程系数公式
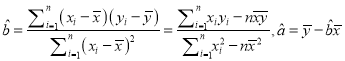 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
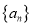 满足
满足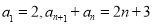 .
.(1)求
 ;
;(2)求
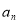 的表达式.
的表达式.
相关试题

