【题目】若对于定义在![]() 上的连续函数
上的连续函数![]() ,存在常数
,存在常数![]() (
(![]() ),使得
),使得![]() 对任意的实数
对任意的实数![]() 成立,则称
成立,则称![]() 是回旋函数,且阶数为
是回旋函数,且阶数为![]() .
.
(1)试判断函数![]() 是否是一个阶数为1的回旋函数,并说明理由;
是否是一个阶数为1的回旋函数,并说明理由;
(2)已知![]() 是回旋函数,求实数
是回旋函数,求实数![]() 的值;
的值;
(3)若回旋函数![]() (
(![]() )在
)在![]() 恰有100个零点,求实数
恰有100个零点,求实数![]() 的值.
的值.
参考答案:
【答案】(1)![]() 是一个阶数为1的回旋函数;(2)
是一个阶数为1的回旋函数;(2)![]() ,
, ![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据“回旋函数”、“阶数”的定义,只需证明![]() 即可;(2)
即可;(2)![]() 是
是![]() 阶回旋函数,则
阶回旋函数,则![]() 恒成立,由三角函数的值域可知
恒成立,由三角函数的值域可知![]() ,然后解简单的三角方程即可得结果;(3)根据“回旋函数”的定义可得,
,然后解简单的三角方程即可得结果;(3)根据“回旋函数”的定义可得, ![]() ,根据正弦函数的周期性结合图象即可得结果.
,根据正弦函数的周期性结合图象即可得结果.
试题解析:(1)![]()
![]() ,
,
![]() 函数
函数![]() 是一个阶数为1的回旋函数.
是一个阶数为1的回旋函数.
(2)设![]() 是
是![]() 阶回旋函数,则
阶回旋函数,则![]() ,
,
若![]() ,上式对任意实数
,上式对任意实数![]() 均成立;
均成立;
若![]() ,
, ![]() ,由三角函数的值域可知
,由三角函数的值域可知![]() ,
,
当![]() 时,对任意实数
时,对任意实数![]() 有
有![]() ;
;
则![]() ,
, ![]() ,所以
,所以![]() .
.
当![]() 时,对任意实数
时,对任意实数![]() 有
有![]() ;
;
则![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() .
.
综上所述: ![]() ,
, ![]() .
.
(3)![]()
![]() ,对任意的
,对任意的![]() 都成立.
都成立.
由(2)可知![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
令![]() ,解得
,解得![]() (
(![]() ).
).
![]() 函数
函数![]() 在
在![]() 恰有100个零点,
恰有100个零点, ![]() ,
,
![]() .又
.又![]() ,
, ![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
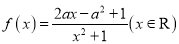 ,其中
,其中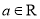 .
.(1)当
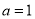 时,求曲线
时,求曲线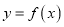 在点
在点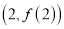 处的切线方程;
处的切线方程;(2)当
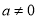 时,求函数
时,求函数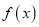 的单调区间与极值.
的单调区间与极值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
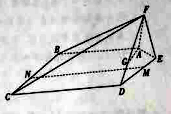
如图,在五棱锥
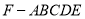 中,
中,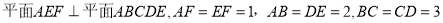 ,且
,且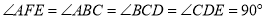 .
.
(1)已知点
 在线段
在线段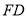 上,确定
上,确定 的位置,使得
的位置,使得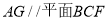 ;
;(2)点
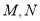 分别在线段
分别在线段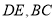 上,若沿直线
上,若沿直线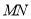 将四边形
将四边形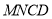 向上翻折,
向上翻折, 与
与 恰好重合,求直线
恰好重合,求直线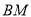 与平面
与平面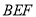 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在透明塑料制成的长方体
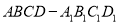 容器内灌进一些水(未满),现将容器底面一边
容器内灌进一些水(未满),现将容器底面一边 固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:
固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:①水的部分始终呈棱柱状;
②水面四边形
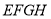 的面积为定值;
的面积为定值;③棱
 始终与水面
始终与水面 平行;
平行;④若
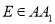 ,
,  ,则
,则 是定值.
是定值.则其中正确命题的个数的是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
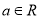 ,函数
,函数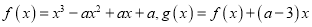 .
.(1)求证:曲线
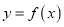 在点
在点 处的切线过定点;
处的切线过定点;(2)若
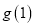 是
是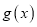 在区间
在区间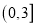 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数 的取值范围;
的取值范围;(3)求证:对任意给定的正数
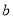 ,总存在
,总存在 ,使得
,使得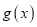 在
在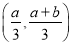 上为单调函数.
上为单调函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 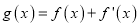
(Ⅰ)求
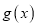 的单调区间和最小值;
的单调区间和最小值;(Ⅱ)讨论
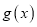 与
与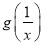 的大小关系;
的大小关系;(Ⅲ)求
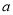 的取值范围,使得
的取值范围,使得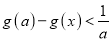 对任意
对任意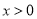 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
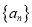 的前
的前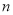 项和为
项和为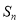 ,且满足
,且满足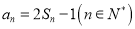 .
.(1)求证:数列
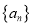 为等比数列;
为等比数列;(2)若
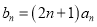 ,求
,求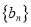 的前
的前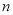 项和
项和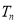 .
.
相关试题

