【题目】设![]() ,
, ![]()
(Ⅰ)求![]() 的单调区间和最小值;
的单调区间和最小值;
(Ⅱ)讨论![]() 与
与![]() 的大小关系;
的大小关系;
(Ⅲ)求![]() 的取值范围,使得
的取值范围,使得![]() 对任意
对任意![]() 成立.
成立.
参考答案:
【答案】(Ⅰ)![]() 的单调减区间是
的单调减区间是![]() ,单调递增区间是
,单调递增区间是![]() ,最小值为
,最小值为![]() ;(II)当
;(II)当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ;(III)
;(III)![]() .
.
【解析】试题分析:(I)求导,并判断导数的符号确定函数的单调区间和极值、最值,即可求得结果;(Ⅱ)通过函数的导数,利用函数的单调性,比较两个函数的大小关系即可;(Ⅲ)利用(Ⅰ)的结论,转化不等式,求解即可.
试题解析:(Ⅰ)由题设知![]() 、
、![]() ,∴
,∴![]() ,令
,令![]() ,得
,得![]()
当![]() 时,
时, ![]() ,故
,故![]() 是
是![]() 的单调减区间.
的单调减区间.
当![]() 时,
时, ![]() ,故
,故![]() 是
是![]() 的单调递增区间,因此,
的单调递增区间,因此, ![]()
是![]() 的唯一值点,且为极小值点,从而是最小值点,所以最小值为
的唯一值点,且为极小值点,从而是最小值点,所以最小值为![]() .
.
(Ⅱ)![]() 设
设![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]() 即
即![]() ,当
,当![]() ,时
,时![]() ,因此在
,因此在![]() 内单调递减,当
内单调递减,当![]() 时,
时, ![]() 即
即![]() .当
.当![]() 时,
时, ![]() 即
即![]()
(Ⅲ)由(Ⅰ)知![]() 的最小值为
的最小值为![]() ,所以,
,所以, ![]() ,对任意
,对任意![]() ,成立
,成立![]() ,即
,即![]() ,从而得
,从而得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在透明塑料制成的长方体
 容器内灌进一些水(未满),现将容器底面一边
容器内灌进一些水(未满),现将容器底面一边 固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:
固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:①水的部分始终呈棱柱状;
②水面四边形
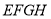 的面积为定值;
的面积为定值;③棱
 始终与水面
始终与水面 平行;
平行;④若
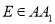 ,
,  ,则
,则 是定值.
是定值.则其中正确命题的个数的是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若对于定义在
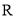 上的连续函数
上的连续函数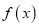 ,存在常数
,存在常数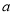 (
(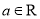 ),使得
),使得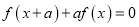 对任意的实数
对任意的实数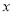 成立,则称
成立,则称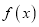 是回旋函数,且阶数为
是回旋函数,且阶数为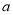 .
.(1)试判断函数
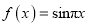 是否是一个阶数为1的回旋函数,并说明理由;
是否是一个阶数为1的回旋函数,并说明理由;(2)已知
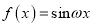 是回旋函数,求实数
是回旋函数,求实数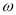 的值;
的值;(3)若回旋函数
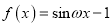 (
(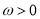 )在
)在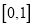 恰有100个零点,求实数
恰有100个零点,求实数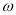 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
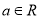 ,函数
,函数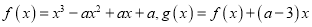 .
.(1)求证:曲线
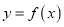 在点
在点 处的切线过定点;
处的切线过定点;(2)若
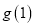 是
是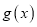 在区间
在区间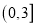 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数 的取值范围;
的取值范围;(3)求证:对任意给定的正数
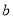 ,总存在
,总存在 ,使得
,使得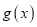 在
在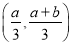 上为单调函数.
上为单调函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
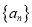 的前
的前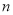 项和为
项和为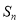 ,且满足
,且满足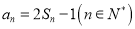 .
.(1)求证:数列
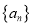 为等比数列;
为等比数列;(2)若
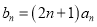 ,求
,求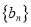 的前
的前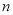 项和
项和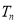 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面几种推理是合情推理的是 ( )
①由圆的性质类比出球的有关性质
②由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180°
③某次考试张军成绩是100分,由此推出全班同学成绩都是100分
④数列1,0,1,0,…,推测出每项公式
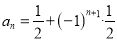
A. ①② B. ①③④ C. ①②④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的年销售量
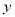 与该年广告费用支出
与该年广告费用支出 有关,现收集了4组观测数据列于下表:
有关,现收集了4组观测数据列于下表: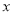 (万元)
(万元)1
4
5
6
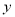 (万元)
(万元)30
40
60
50
现确定以广告费用支出
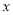 为解释变量,销售量
为解释变量,销售量 为预报变量对这两个变量进行统计分析.
为预报变量对这两个变量进行统计分析.(1)已知这两个变量满足线性相关关系,试建立
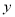 与
与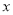 之间的回归方程;
之间的回归方程;(2)假如2017年广告费用支出为10万元,请根据你得到的模型,预测该年的销售量
 .
.(线性回归方程系数公式
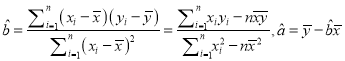 ).
).
相关试题

