【题目】设函数 ![]() ,若曲线
,若曲线 ![]() 上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
A.[0,e2﹣e+1]
B.[0,e2+e﹣1]
C.[0,e2+e+1]
D.[0,e2﹣e﹣1]
参考答案:
【答案】D
【解析】解:∵﹣1≤cosx≤1,∴ ![]() 的最大值为e,最小值为1,∴1≤y0≤e, 显然f(x)=
的最大值为e,最小值为1,∴1≤y0≤e, 显然f(x)= ![]() 是增函数,
是增函数,
(i)若f(y0)>y0 , 则f(f(y0))>f(y0)>y0 , 与f(f(y0))=y0矛盾;
(ii)若f(y0)<y0 , 则f(f(y0))<f(y0)<y0 , 与f(f(y0))=y0矛盾;
∴f(y0)=y0 ,
∴y0为方程f(x)=x的解,即方程f(x)=x在[1,e]上有解,
由f(x)=x得m=x2﹣x﹣lnx,
令g(x)=x2﹣x﹣lnx,x∈[1,e],
则g′(x)=2x﹣1﹣ ![]() =
= ![]() =
= ![]() ,
,
∴当x∈[1,e]时,g′(x)≥0,
∴g(x)在[1,e]上单调递增,
∴gmin(x)=g(1)=0,gmax(x)=g(e)=e2﹣e﹣1,
∴0≤m≤e2﹣e﹣1.
故选D.
求出y0的范围,证明f(y0)=y0 , 得出f(x)=x在[1,e]上有解,再分离参数,利用函数单调性求出m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中心在原点的椭圆C1与双曲线C2具有相同的焦点,F1(﹣c,0),F2(c,0),P为C1与C2在第一象限的交点,|PF1|=|F1F2|且|PF2|=5,若椭圆C1的离心率
 ,则双曲线的离心率e2的范围是( )
,则双曲线的离心率e2的范围是( )
A.
B.
C.(2,3)
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC,
 ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为  ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.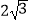
D.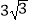
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
 的渐近线方程为
的渐近线方程为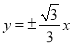 ,左焦点为F,过
,左焦点为F,过 的直线为
的直线为 ,原点到直线
,原点到直线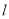 的距离是
的距离是
(1)求双曲线的方程;
(2)已知直线
 交双曲线于不同的两点C,D,问是否存在实数
交双曲线于不同的两点C,D,问是否存在实数 ,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由。
,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, .
. 若
若 ,解不等式
,解不等式 ;
; 若不等式
若不等式 对一切实数x恒成立,求实数a的取值范围;
对一切实数x恒成立,求实数a的取值范围; 若
若 ,解不等式
,解不等式 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱柱
 中,
中,  平面
平面 ,
,  ,
,  ,
,  为
为 的中点.
的中点.
(1)求四棱锥
 的体积;
的体积;(2)求证:
 ;
;(3)判断线段
 上是否存在一点
上是否存在一点 (与点
(与点 不重合),使得
不重合),使得 四点共面? (结论不要求证明)
四点共面? (结论不要求证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】平面上,点A、C为射线PM上的两点,点B、D为射线PN上的两点,则有
 (其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有
(其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有  =(其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积).
=(其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积). 
相关试题

