【题目】中心在原点的椭圆C1与双曲线C2具有相同的焦点,F1(﹣c,0),F2(c,0),P为C1与C2在第一象限的交点,|PF1|=|F1F2|且|PF2|=5,若椭圆C1的离心率 ![]() ,则双曲线的离心率e2的范围是( )
,则双曲线的离心率e2的范围是( )
A.![]()
B.![]()
C.(2,3)
D.![]()
参考答案:
【答案】C
【解析】解:设椭圆的方程为 ![]() +
+ ![]() =1(a>b>0), 其离心率为e1 ,
=1(a>b>0), 其离心率为e1 ,
双曲线的方程为 ![]() ﹣
﹣ ![]() =1(m>0,n>0),其离心率为e2 ,
=1(m>0,n>0),其离心率为e2 ,
|F1F2|=2c,
∵有公共焦点的椭圆与双曲线在第一象限的交点为P,
△PF1F2是以PF2为底边的等腰三角形,
∴在椭圆中,|PF1|+|PF2|=2a,而|PF1|=|F1F2|=2c,
∴|PF2|=2a﹣2c,①
同理,在该双曲线中,|PF2|=2c﹣2m;②
由①②可得m=2c﹣a.
∵e1= ![]() ∈(
∈( ![]() ,
, ![]() ),
),
∴ ![]() <
< ![]() <
< ![]() ,
,
又e2= ![]() =
= ![]() =
= ![]() =
= ![]() ∈(2,3).
∈(2,3).
故选:C.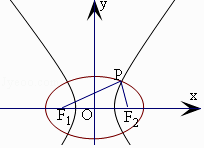
设椭圆的方程为 ![]() +
+ ![]() =1(a>b>0)(a>b>0),其离心率e1 , 双曲线的方程为
=1(a>b>0)(a>b>0),其离心率e1 , 双曲线的方程为 ![]() ﹣
﹣ ![]() =1(m>0,n>0),离心率为e2 , 由e1=
=1(m>0,n>0),离心率为e2 , 由e1= ![]() ∈(
∈( ![]() ,
, ![]() ),e2=
),e2= ![]() ,由△PF1F2是以PF2为底边的等腰三角形,结合椭圆与双曲线的定义可求得m=2c﹣a,从而可求得答案.
,由△PF1F2是以PF2为底边的等腰三角形,结合椭圆与双曲线的定义可求得m=2c﹣a,从而可求得答案.
-
科目: 来源: 题型:
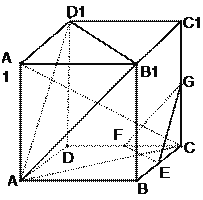
查看答案和解析>>【题目】如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求直线
 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:
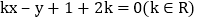
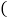 1
1 证明直线l经过定点并求此点的坐标;
证明直线l经过定点并求此点的坐标; 2
2 若直线l不经过第四象限,求k的取值范围;
若直线l不经过第四象限,求k的取值范围; 3
3 若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设
若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设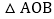 的面积为S,求S的最小值及此时直线l的方程.
的面积为S,求S的最小值及此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知极点为直角坐标系的原点,极轴为x轴正半轴且单位长度相同的极坐标系中曲线C1:ρ=1,
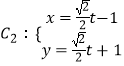 (t为参数).
(t为参数).
(Ⅰ)求曲线C1上的点到曲线C2距离的最小值;
(Ⅱ)若把C1上各点的横坐标都扩大为原来的2倍,纵坐标扩大为原来的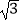 倍,得到曲线
倍,得到曲线 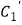 .设P(﹣1,1),曲线C2与
.设P(﹣1,1),曲线C2与 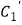 交于A,B两点,求|PA|+|PB|.
交于A,B两点,求|PA|+|PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC,
 ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为  ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.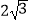
D.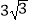
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
 的渐近线方程为
的渐近线方程为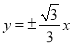 ,左焦点为F,过
,左焦点为F,过 的直线为
的直线为 ,原点到直线
,原点到直线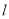 的距离是
的距离是
(1)求双曲线的方程;
(2)已知直线
 交双曲线于不同的两点C,D,问是否存在实数
交双曲线于不同的两点C,D,问是否存在实数 ,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由。
,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
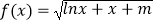 ,若曲线
,若曲线 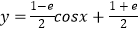 上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
A.[0,e2﹣e+1]
B.[0,e2+e﹣1]
C.[0,e2+e+1]
D.[0,e2﹣e﹣1]
相关试题

