【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC, ![]() ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为 ![]() ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:设AC的中点为D,连接BD,PD,则PD⊥平面ABC, ∵△ABC是等腰直角三角形,∴外接球的球心O在PD上,
设AB=BC=a,PD=h,外接球半径OC=OP=R,
则OD=h﹣R,CD= ![]() AC=
AC= ![]() a,
a,
∵VP﹣ABC= ![]() =
= ![]() =
= ![]() ,∴a2=
,∴a2= ![]() ,
,
∵CD2+OD2=OC2 , 即(h﹣R)2+ ![]() a2=R2 ,
a2=R2 ,
∴R= ![]() =
= ![]() =
= ![]() ≥3
≥3 ![]() =
= ![]() ,
,
当且仅当 ![]() 即h=3时取等号,
即h=3时取等号,
∴当外接球半径取得最小值时,h=3.
故选:B.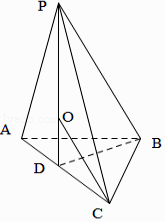
设AB=a,棱锥的高为h,根据体积得出a与h的关系,根据勾股定理得出外接球半径R关于h的表达式,利用基本不等式得出R最小值时对应的h的值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:
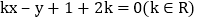
 1
1 证明直线l经过定点并求此点的坐标;
证明直线l经过定点并求此点的坐标; 2
2 若直线l不经过第四象限,求k的取值范围;
若直线l不经过第四象限,求k的取值范围; 3
3 若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设
若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设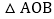 的面积为S,求S的最小值及此时直线l的方程.
的面积为S,求S的最小值及此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知极点为直角坐标系的原点,极轴为x轴正半轴且单位长度相同的极坐标系中曲线C1:ρ=1,
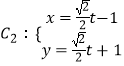 (t为参数).
(t为参数).
(Ⅰ)求曲线C1上的点到曲线C2距离的最小值;
(Ⅱ)若把C1上各点的横坐标都扩大为原来的2倍,纵坐标扩大为原来的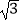 倍,得到曲线
倍,得到曲线 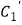 .设P(﹣1,1),曲线C2与
.设P(﹣1,1),曲线C2与 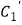 交于A,B两点,求|PA|+|PB|.
交于A,B两点,求|PA|+|PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】中心在原点的椭圆C1与双曲线C2具有相同的焦点,F1(﹣c,0),F2(c,0),P为C1与C2在第一象限的交点,|PF1|=|F1F2|且|PF2|=5,若椭圆C1的离心率
 ,则双曲线的离心率e2的范围是( )
,则双曲线的离心率e2的范围是( )
A.
B.
C.(2,3)
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
 的渐近线方程为
的渐近线方程为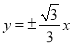 ,左焦点为F,过
,左焦点为F,过 的直线为
的直线为 ,原点到直线
,原点到直线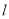 的距离是
的距离是
(1)求双曲线的方程;
(2)已知直线
 交双曲线于不同的两点C,D,问是否存在实数
交双曲线于不同的两点C,D,问是否存在实数 ,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由。
,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
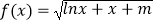 ,若曲线
,若曲线 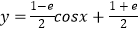 上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
A.[0,e2﹣e+1]
B.[0,e2+e﹣1]
C.[0,e2+e+1]
D.[0,e2﹣e﹣1] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, .
. 若
若 ,解不等式
,解不等式 ;
; 若不等式
若不等式 对一切实数x恒成立,求实数a的取值范围;
对一切实数x恒成立,求实数a的取值范围; 若
若 ,解不等式
,解不等式 .
.
相关试题

