【题目】已知抛物线![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求抛物线的方程;
(Ⅱ)设![]() 和
和![]() 为抛物线上的两个动点,其中
为抛物线上的两个动点,其中![]() 且
且![]() ,线段
,线段![]() 的垂直平分线
的垂直平分线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() .
.
【解析】试题分析:(1)先根据导数几何意义得![]() ,再根据切点在切线上,解方程组得
,再根据切点在切线上,解方程组得![]() (2)设线段
(2)设线段![]() 中点
中点![]() ,根据斜率公式得
,根据斜率公式得![]() ,根据点斜式得线段
,根据点斜式得线段![]() 的垂直平分线
的垂直平分线![]() 方程,解得T坐标,利用点到点到直线距离公式得高,联立直线方程与抛物线方程,利用韦达定理以及弦长公式得底|AB|,根据三角形面积公式得面积函数关系,最后根据均值不等式求最值
方程,解得T坐标,利用点到点到直线距离公式得高,联立直线方程与抛物线方程,利用韦达定理以及弦长公式得底|AB|,根据三角形面积公式得面积函数关系,最后根据均值不等式求最值
试题解析:(Ⅰ)设点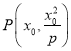 ,由
,由![]() 得
得![]() ,求导
,求导![]() ,
,
因为直线![]() 的斜率为-1,所以
的斜率为-1,所以![]() 且
且![]() ,解得
,解得![]() ,
,
所以抛物线的方程为![]() .
.
(Ⅱ)设线段![]() 中点
中点![]() ,则
,则![]()
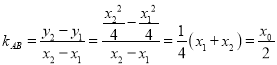 ,
,
∴直线l的方程为![]() ,
,
即![]() ,
, ![]() 过定点
过定点![]() .
.
联立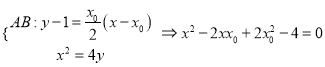
得![]() ,
,
![]()
![]()
![]() ,
,
设![]() 到AB的距离
到AB的距离![]() ,
,
![]()
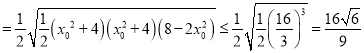 ,
,
当且仅当![]() ,即
,即![]() (-2,2)时取等号,
(-2,2)时取等号,
![]() 的最大值为
的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本2500万元,每生产x(百辆),需另投入成本
 万元,且
万元,且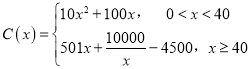 .由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.(1)求出2018年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
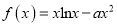 .
.(1)若
 有两个零点,求
有两个零点,求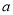 的范围;
的范围;(2)若
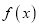 有两个极值点,求
有两个极值点,求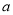 的范围;
的范围;(3)在(2)的条件下,若
 的两个极值点为
的两个极值点为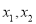
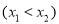 ,求证:
,求证: 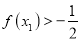 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
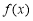 满足以下两个条件:①不等式
满足以下两个条件:①不等式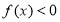 的解集是
的解集是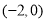 ②函数
②函数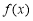 在
在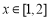 上的最小值是3.
上的最小值是3.(Ⅰ)求
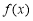 的解析式;
的解析式;(Ⅱ)若点
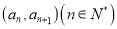 在函数
在函数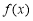 的图象上,且
的图象上,且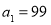 .
.(ⅰ)求证:数列
 为等比数列
为等比数列(ⅱ)令
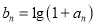 ,是否存在正实数
,是否存在正实数 ,使不等式
,使不等式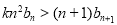 对于一切的
对于一切的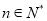 恒成立?若存在,指出
恒成立?若存在,指出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形
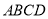 的边长为2,
的边长为2,  .
. 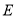 是边
是边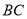 上一点,线段
上一点,线段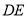 交
交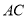 于点
于点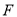 .
.(1)若
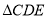 的面积为
的面积为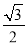 ,求
,求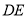 的长;
的长;(2)若
 ,求
,求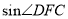 .
. -
科目: 来源: 题型:
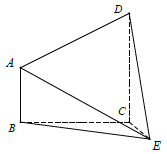
查看答案和解析>>【题目】如图,在四棱锥
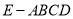 中,
中, 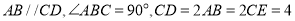 ,
,  .
.
(1)证明:平面
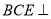 平面
平面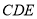 ;
;(2)若
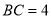 ,求二面角
,求二面角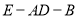 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我校为了让高一学生更有效率地利用周六的时间,在高一新生第一次摸底考试后采取周六到校自主学习,同时由班主任老师值班,家长轮流值班.一个月后进行了第一次月考,高一数学教研组通过系统抽样抽取了
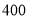 名学生,并统计了他们这两次数学考试的优良人数和非优良人数,其中部分统计数据如下:
名学生,并统计了他们这两次数学考试的优良人数和非优良人数,其中部分统计数据如下:
(1)请画出这次调查得到的
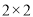 列联表;并判定能否在犯错误概率不超过
列联表;并判定能否在犯错误概率不超过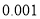 的前提下认为周六到校自习对提高学生成绩有效?
的前提下认为周六到校自习对提高学生成绩有效?(2)从这组学生摸底考试中数学优良成绩中和第一次月考的数学非优良成绩中,按分层抽样随机抽取
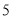 个成绩,再从这
个成绩,再从这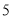 个成绩中随机抽取
个成绩中随机抽取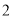 个,求这
个,求这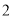 个成绩来自同一次考试的概率.
个成绩来自同一次考试的概率.下面是临界值表供参考:

(参考公式:
 ,其中
,其中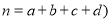
相关试题

