【题目】已知![]() .
.
(1)若![]() 有两个零点,求
有两个零点,求![]() 的范围;
的范围;
(2)若![]() 有两个极值点,求
有两个极值点,求![]() 的范围;
的范围;
(3)在(2)的条件下,若![]() 的两个极值点为
的两个极值点为![]()
![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】(1) ![]() (2)
(2) ![]() (3) 见解析
(3) 见解析
【解析】试题分析:(1)由题意函数![]() 必有极值点,且极大值大于零,列对应不等式,解得
必有极值点,且极大值大于零,列对应不等式,解得![]() 的范围;(2)先求导数,得
的范围;(2)先求导数,得![]() 有两个改变
有两个改变![]() 符号的零点,即导函数
符号的零点,即导函数![]() 必有极值点,且极大值大于零,列对应不等式,解得
必有极值点,且极大值大于零,列对应不等式,解得![]() 的范围;(3)由(2)
的范围;(3)由(2)![]() 再利用极值点条件构造函数
再利用极值点条件构造函数![]() ,最后利用导数研究函数单调性,根据最值证不等式
,最后利用导数研究函数单调性,根据最值证不等式
试题解析:方法一:
(1)![]()
![]() 有两个零点,
有两个零点, ![]() 有两个零点
有两个零点
![]()
![]() 时
时![]() 在
在![]() 上单调,最多有一个零点,不合题意
上单调,最多有一个零点,不合题意
![]() 在
在![]() 上↑,在
上↑,在![]() 上↓
上↓
![]()
又![]() 时,
时, ![]()
![]() 必有两个零点
必有两个零点
![]()
(2)![]() 有两个改变
有两个改变![]() 符号的零点
符号的零点
设![]() 则
则![]()
![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 在
在![]() 上单调,最多有一个零点,不合题意
上单调,最多有一个零点,不合题意
![]() 由
由![]() 得:
得: ![]() ,
,
![]() 在
在![]() 上↑,在
上↑,在![]() 上↓
上↓
![]() ,即
,即![]()
又![]()
![]() 在
在![]() 各有一个零点
各有一个零点
![]()
(3)由(2),结合h(1)=1-2a>0,知![]()
![]()
设![]()
![]() 在
在![]() 上↓,
上↓,![]()
![]()
方法二:分离参数法
(1)![]() ,两图象有两交点
,两图象有两交点
令![]()
当![]()
当![]() ,
, ![]()
结合图像, ![]() 。
。
(2)![]() 有两个改变
有两个改变![]() 符号的零点
符号的零点
等价于![]() 对应的两函数的图像有两交点
对应的两函数的图像有两交点
令![]()
当![]()
当![]()
结合图象, ![]()
(3)由(2)![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度
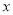 (单位:℃),对某种鸡的时段产蛋量
(单位:℃),对某种鸡的时段产蛋量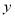 (单位:
(单位: 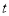 )和时段投入成本
)和时段投入成本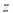 (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度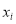 和产蛋量
和产蛋量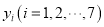 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
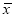
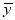

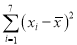
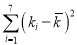
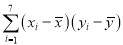
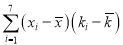
17.40
82.30
3.6
140
9.7
2935.1
35.0
其中
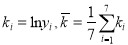 .
.(1)根据散点图判断,
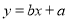 与
与 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量 关于鸡舍时段控制温度
关于鸡舍时段控制温度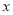 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)(2)若用
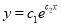 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立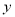 关于
关于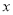 的回归方程;
的回归方程;(3)已知时段投入成本
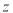 与
与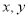 的关系为
的关系为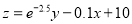 ,当时段控制温度为28℃时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
,当时段控制温度为28℃时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?附:①对于一组具有有线性相关关系的数据
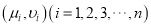 ,其回归直线
,其回归直线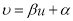 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为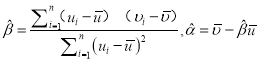
②
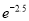
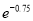
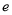
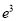
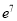
0.08
0.47
2.72
20.09
1096.63
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率
的离心率 ,且经过点
,且经过点 .
.(1)求椭圆方程;
(2)过点
 的直线与椭圆交于
的直线与椭圆交于 两个不同的点,求线段
两个不同的点,求线段 的垂直平分线在
的垂直平分线在 轴截距的范围.
轴截距的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本2500万元,每生产x(百辆),需另投入成本
 万元,且
万元,且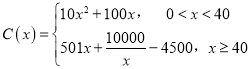 .由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.(1)求出2018年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
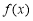 满足以下两个条件:①不等式
满足以下两个条件:①不等式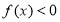 的解集是
的解集是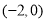 ②函数
②函数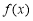 在
在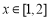 上的最小值是3.
上的最小值是3.(Ⅰ)求
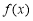 的解析式;
的解析式;(Ⅱ)若点
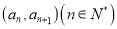 在函数
在函数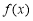 的图象上,且
的图象上,且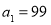 .
.(ⅰ)求证:数列
 为等比数列
为等比数列(ⅱ)令
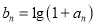 ,是否存在正实数
,是否存在正实数 ,使不等式
,使不等式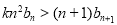 对于一切的
对于一切的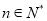 恒成立?若存在,指出
恒成立?若存在,指出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
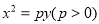 上点
上点 处的切线方程为
处的切线方程为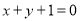 .
. (Ⅰ)求抛物线的方程;
(Ⅱ)设
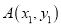 和
和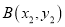 为抛物线上的两个动点,其中
为抛物线上的两个动点,其中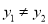 且
且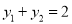 ,线段
,线段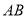 的垂直平分线
的垂直平分线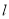 与
与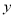 轴交于点
轴交于点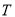 ,求
,求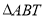 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形
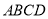 的边长为2,
的边长为2,  .
. 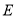 是边
是边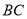 上一点,线段
上一点,线段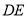 交
交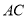 于点
于点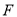 .
.(1)若
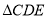 的面积为
的面积为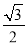 ,求
,求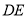 的长;
的长;(2)若
 ,求
,求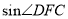 .
.
相关试题

