【题目】已知二次函数![]() 满足以下两个条件:①不等式
满足以下两个条件:①不等式![]() 的解集是
的解集是![]() ②函数
②函数![]() 在
在![]() 上的最小值是3.
上的最小值是3.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若点![]() 在函数
在函数![]() 的图象上,且
的图象上,且![]() .
.
(ⅰ)求证:数列![]() 为等比数列
为等比数列
(ⅱ)令![]() ,是否存在正实数
,是否存在正实数![]() ,使不等式
,使不等式![]() 对于一切的
对于一切的![]() 恒成立?若存在,指出
恒成立?若存在,指出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)(ⅰ)证明过程见解析;(ⅱ)
;(Ⅱ)(ⅰ)证明过程见解析;(ⅱ)![]()
【解析】
(Ⅰ)根据不等式的解集可知函数![]() 与x轴的交点横坐标为
与x轴的交点横坐标为![]() ,0且开口向上,根据对称轴判断函数在
,0且开口向上,根据对称轴判断函数在![]() 上的最小值列出等式求解即可;(Ⅱ)(ⅰ)点
上的最小值列出等式求解即可;(Ⅱ)(ⅰ)点![]() 代入函数并整理得
代入函数并整理得![]() ,同时取对数即可得证;(ⅱ)求出
,同时取对数即可得证;(ⅱ)求出![]() 的通项公式代入不等式可得
的通项公式代入不等式可得![]() 对于一切的
对于一切的![]() 恒成立,利用二次函数的图象与性质求出
恒成立,利用二次函数的图象与性质求出![]() 的最大值即可得解.
的最大值即可得解.
(Ⅰ)因为不等式![]() 的解集是
的解集是![]() ,
,
所以设![]() ,且函数的对称轴为:
,且函数的对称轴为:![]() ,
,
因为![]() 在
在![]() 上单调递增,所以最小值为
上单调递增,所以最小值为![]() ,解得
,解得![]() ,
,
函数解析式为![]() ;
;
(Ⅱ)(ⅰ)证明:因为点![]() 在函数
在函数![]() 的图象上,
的图象上,
所以![]() ,则
,则![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
数列![]() 是以2为首项,2为公比的等比数列;
是以2为首项,2为公比的等比数列;
(ⅱ)![]() ,要使不等式
,要使不等式![]() 对于一切的
对于一切的![]() 恒成立,
恒成立,
则![]() 对于一切的
对于一切的![]() 恒成立,
恒成立,
所以![]() 对于一切的
对于一切的![]() 恒成立,
恒成立,
令![]() ,
,
令![]() ,则
,则![]() ,(
,(![]() ),
),![]() ,
,
所以当![]() 时, 不等式
时, 不等式![]() 对于一切的
对于一切的![]() 恒成立.
恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率
的离心率 ,且经过点
,且经过点 .
.(1)求椭圆方程;
(2)过点
 的直线与椭圆交于
的直线与椭圆交于 两个不同的点,求线段
两个不同的点,求线段 的垂直平分线在
的垂直平分线在 轴截距的范围.
轴截距的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本2500万元,每生产x(百辆),需另投入成本
 万元,且
万元,且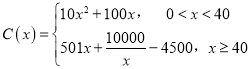 .由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.(1)求出2018年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
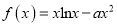 .
.(1)若
 有两个零点,求
有两个零点,求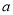 的范围;
的范围;(2)若
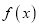 有两个极值点,求
有两个极值点,求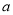 的范围;
的范围;(3)在(2)的条件下,若
 的两个极值点为
的两个极值点为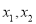
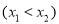 ,求证:
,求证: 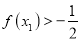 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
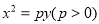 上点
上点 处的切线方程为
处的切线方程为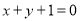 .
. (Ⅰ)求抛物线的方程;
(Ⅱ)设
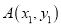 和
和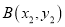 为抛物线上的两个动点,其中
为抛物线上的两个动点,其中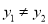 且
且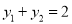 ,线段
,线段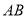 的垂直平分线
的垂直平分线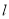 与
与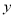 轴交于点
轴交于点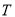 ,求
,求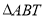 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形
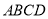 的边长为2,
的边长为2,  .
. 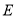 是边
是边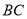 上一点,线段
上一点,线段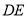 交
交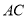 于点
于点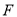 .
.(1)若
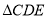 的面积为
的面积为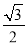 ,求
,求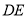 的长;
的长;(2)若
 ,求
,求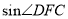 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
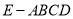 中,
中, 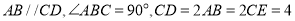 ,
,  .
.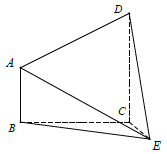
(1)证明:平面
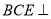 平面
平面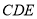 ;
;(2)若
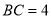 ,求二面角
,求二面角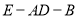 的余弦值.
的余弦值.
相关试题

