【题目】已知菱形![]() 的边长为2,
的边长为2, ![]() .
. ![]() 是边
是边![]() 上一点,线段
上一点,线段![]() 交
交![]() 于点
于点![]() .
.
(1)若![]() 的面积为
的面积为![]() ,求
,求![]() 的长;
的长;
(2)若![]() ,求
,求![]() .
.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由面积公式![]() 求出
求出![]() ,再根据余弦定理,计算得
,再根据余弦定理,计算得![]() (2)法一:设
(2)法一:设![]() 在
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,求得
,求得![]() ,利用
,利用![]() 即可求出结果;法二:设
即可求出结果;法二:设![]() ,设
,设![]() 则
则![]() 由余弦定理,得
由余弦定理,得![]() ,代入解得解得
,代入解得解得![]() ,或
,或![]() ,验证得
,验证得![]() ,再由正弦定理,得
,再由正弦定理,得![]() 计算出结果
计算出结果
解析:解法一:(1)依题意,得![]() ,
,
因为![]() 的面积
的面积![]() ,
,
所以![]() ,
,
所以![]() ,
,
解得![]() ,
,
根据余弦定理,得![]()
![]() .
.
(2)依题意,得![]() ,设
,设![]() ,则
,则![]() ,
,
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,
,
因为![]() ,
,
所以![]() ,
,
所以![]()
所以![]() .
.
解法二:(1)同解法一.
(2)依题意,得![]() ,设
,设![]() ,则
,则![]() ,
,
在![]() 中,设
中,设![]() ,因为
,因为![]() ,则
,则![]() ,
,
由余弦定理,得![]() ,
,
得![]() ,
,
解得![]() ,或
,或![]() .
.
又因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,
在![]() 中,由正弦定理,得
中,由正弦定理,得![]() ,
,
得 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线  的参数方程为
的参数方程为  (其中
(其中  为参数),曲线
为参数),曲线  :
: 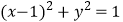 ,以坐标原点
,以坐标原点  为极点,
为极点,  轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线 的普通方程和曲线
的普通方程和曲线  的极坐标方程;
的极坐标方程;
(2)若射线 (
(  )与曲线
)与曲线  ,
,  分别交于
分别交于  ,
,  两点,求
两点,求  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是自然对数的底数,
是自然对数的底数,  .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若 为整数,
为整数,  ,且当
,且当  时,
时,  恒成立,其中
恒成立,其中  为
为  的导函数,求
的导函数,求  的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知各项均为正数的数列
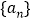 满足
满足 , 且
, 且 ,其中
,其中 .
.(1) 求数列
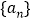 的通项公式;
的通项公式;(2) 设数列{bn}满足 bn=
 ,是否存在正整数
,是否存在正整数 ,使得b1,bm,bn成等比数列?若存在,求出所有的
,使得b1,bm,bn成等比数列?若存在,求出所有的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3) 令
 ,记数列{cn}的前
,记数列{cn}的前 项和为
项和为 ,其中
,其中 ,证明:
,证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,  底面
底面  ,底面
,底面  为直角梯形,
为直角梯形, 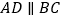 ,
,  ,
,  ,
,  为
为  的中点,平面
的中点,平面  交
交  于
于  点.、
点.、
(1)求证: ;
;
(2)求二面角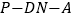 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正四面体的“骰子”(四个面分别标有1,2,3,4四个数字),掷一次“骰子”三个侧面的数字的和为“点数”,连续抛掷“骰子”两次.
(1)设A为事件“两次掷‘骰子’的点数和为16”,求事件A发生的概率;
(2)设X为两次掷“骰子”的点数之差的绝对值,求随机变量X的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为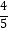 .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为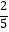 ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金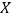 (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
相关试题

