【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]()
(1) 求点P的轨迹方程;
(2)设点![]() 在直线x=-3上,且
在直线x=-3上,且![]() .证明过点P且垂直于OQ的直线l过C的左焦点F.
.证明过点P且垂直于OQ的直线l过C的左焦点F.
参考答案:
【答案】(1)![]()
(2) 由题意知F(-1,0),设Q(-3,t),P(m,n),则
![]() ,
,
![]() .
.
由![]() 得-3m-
得-3m-![]() +tn-
+tn-![]() =1,又由(1)知
=1,又由(1)知![]() ,故
,故
3+3m-tn=0.
所以![]() ,即
,即![]() .又过点P存在唯一直线垂直于OQ,所以过点P且垂直于OQ的直线l过C的左焦点F.
.又过点P存在唯一直线垂直于OQ,所以过点P且垂直于OQ的直线l过C的左焦点F.
【解析】
(1)设P(x,y),M(![]() ),则N(
),则N(![]() ),
),![]()
由![]() 得
得![]() .
.
因为M(![]() )在C上,所以
)在C上,所以![]() .
.
因此点P的轨迹为![]() .
.
(2) 由题意知F(-1,0),设Q(-3,t),P(m,n),则
![]() ,
,
![]() .
.
由![]() 得-3m-
得-3m-![]() +tn-
+tn-![]() =1,又由(1)知
=1,又由(1)知![]() ,故
,故
3+3m-tn=0.
所以![]() ,即
,即![]() .又过点P存在唯一直线垂直于OQ,所以过点P且垂直于OQ的直线l过C的左焦点F.
.又过点P存在唯一直线垂直于OQ,所以过点P且垂直于OQ的直线l过C的左焦点F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,若存在△A1B1C1 , 满足
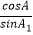 =
= 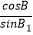 =
= 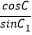 =1,则称△A1B1C1是△ABC的一个“友好”三角形.在满足下述条件的三角形中,存在“友好”三角形的是:(请写出符合要求的条件的序号) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°.
=1,则称△A1B1C1是△ABC的一个“友好”三角形.在满足下述条件的三角形中,存在“友好”三角形的是:(请写出符合要求的条件的序号) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(1-x2)ex.
(1)讨论f(x)的单调性;
(2)当x
 0时,f(x)
0时,f(x) ax+1,求a的取值范围.
ax+1,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn .
(1)求数列{an}的通项公式an及Sn;
(2)若等比数列{bn}的前n项和为Tn , 且b1=2,b4=S4 , 求Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
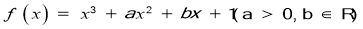 有极值,且导函数
有极值,且导函数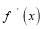 的极值点是
的极值点是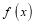 的零点。(极值点是指函数取极值时对应的自变量的值)
的零点。(极值点是指函数取极值时对应的自变量的值)求b关于a的函数关系式,并写出定义域;
证明:b>3a;
若
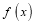 ,
,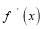 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于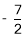 ,求a的取值范围。
,求a的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,椭圆
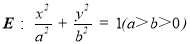 的左、右焦点分别为F1,F2,离心率为
的左、右焦点分别为F1,F2,离心率为 ,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.(1)求椭圆E的标准方程;
(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.
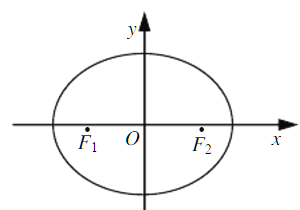
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
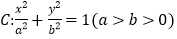 的短轴长为
的短轴长为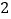 ,椭圆
,椭圆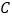 上任意一点到右焦点
上任意一点到右焦点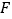 距 离的最大值为
距 离的最大值为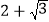 .
.(Ⅰ)求椭圆
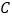 的标准方程;
的标准方程;(Ⅱ)过点
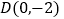 作直线
作直线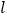 与曲线
与曲线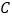 交于
交于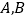 两点,点
两点,点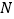 满足
满足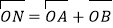 (
(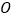 为坐标原点),求四边形
为坐标原点),求四边形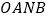 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线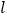 的方程.
的方程.
相关试题

