【题目】设函数f(x)=(1-x2)ex.
(1)讨论f(x)的单调性;
(2)当x![]() 0时,f(x)
0时,f(x)![]() ax+1,求a的取值范围.
ax+1,求a的取值范围.
参考答案:
【答案】(1)单调递增
(2)[1,+∞)
【解析】
(1)f ’(x)=(1-2x-x2)ex
令f’(x)=0得x=-1-![]() ,x=-1+
,x=-1+![]()
当x∈(-∞,-1-![]() )时,f’(x)<0;当x∈(-1-
)时,f’(x)<0;当x∈(-1-![]() ,-1+
,-1+![]() )时,f’(x)>0;当x∈(-1-
)时,f’(x)>0;当x∈(-1-![]() ,+∞)时,f’(x)<0
,+∞)时,f’(x)<0
所以f(x)在(-∞,-1-![]() ),(-1+
),(-1+![]() ,+∞)单调递减,在(-1-
,+∞)单调递减,在(-1-![]() ,-1+
,-1+![]() )单调递增
)单调递增
(2) f (x)=(1+x)(1-x)ex
当a≥1时,设函数h(x)=(1-x)ex,h’(x)= -xex<0(x>0),因此h(x)在[0,+∞)单调递减,而h(0)=1,
故h(x)≤1,所以
f(x)=(x+1)h(x)≤x+1≤ax+1
当0<a<1时,设函数g(x)=ex-x-1,g’(x)=ex-1>0(x>0),所以g(x)在在[0,+∞)单调递增,而g(0)=0,故ex≥x+1
当0<x<1,![]() ,
,![]() ,取
,取![]()
则![]()
当 ![]()
综上,a的取值范围[1,+∞)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用an表示自然数n的所有因数中最大的那个奇数,例如:9的因数有1,3,9,则a9=9;10的因数有1,2,5,10,则a10=5,记数列{an}的前n项和为Sn , 则S
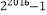 = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:
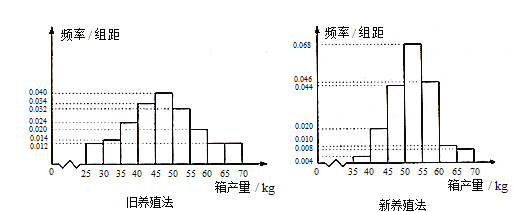
(1) 记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2) 填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg
箱产量≥50kg
旧养殖法
新养殖法
(3) 根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较。
附:
P(
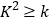 )
)0.050
0.010
0.001
k
3.841
6.635
10.828
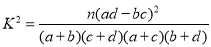

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,若存在△A1B1C1 , 满足
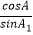 =
= 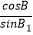 =
= 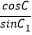 =1,则称△A1B1C1是△ABC的一个“友好”三角形.在满足下述条件的三角形中,存在“友好”三角形的是:(请写出符合要求的条件的序号) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°.
=1,则称△A1B1C1是△ABC的一个“友好”三角形.在满足下述条件的三角形中,存在“友好”三角形的是:(请写出符合要求的条件的序号) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn .
(1)求数列{an}的通项公式an及Sn;
(2)若等比数列{bn}的前n项和为Tn , 且b1=2,b4=S4 , 求Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】设O为坐标原点,动点M在椭圆C
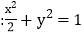 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足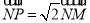
(1) 求点P的轨迹方程;
(2)设点
 在直线x=-3上,且
在直线x=-3上,且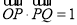 .证明过点P且垂直于OQ的直线l过C的左焦点F.
.证明过点P且垂直于OQ的直线l过C的左焦点F. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
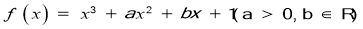 有极值,且导函数
有极值,且导函数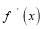 的极值点是
的极值点是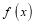 的零点。(极值点是指函数取极值时对应的自变量的值)
的零点。(极值点是指函数取极值时对应的自变量的值)求b关于a的函数关系式,并写出定义域;
证明:b>3a;
若
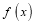 ,
,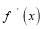 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于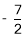 ,求a的取值范围。
,求a的取值范围。
相关试题

