【题目】如图,在平面直角坐标系xOy中,椭圆![]() 的左、右焦点分别为F1,F2,离心率为
的左、右焦点分别为F1,F2,离心率为![]() ,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
(1)求椭圆E的标准方程;
(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.
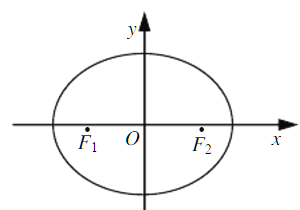
参考答案:
【答案】(1)∵椭圆E的离心率为![]() ,∴
,∴![]() ①.∵两准线之间的距离为8,∴
①.∵两准线之间的距离为8,∴![]() ②.联立①②得
②.联立①②得![]() ,∴
,∴![]() ,故椭圆E的标准方程为
,故椭圆E的标准方程为![]() .
.
(2)设![]() ,则
,则![]() ,由题意得
,由题意得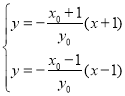 ,整理得
,整理得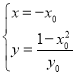 ,∵点
,∵点![]() 在椭圆E上,∴
在椭圆E上,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,故点P的坐标是
,故点P的坐标是![]() .
.
【解析】
解:(1)设椭圆的半焦距为c.
因为椭圆E的离心率为![]() ,两准线之间的距离为8,所以
,两准线之间的距离为8,所以![]() ,
,![]() ,
,
解得![]() ,于是
,于是![]() ,
,
因此椭圆E的标准方程是![]() .
.
(2)由(1)知,![]() ,
,![]() .
.
设![]() ,因为点
,因为点![]() 为第一象限的点,故
为第一象限的点,故![]() .
.
当![]() 时,
时,![]() 与
与![]() 相交于
相交于![]() ,与题设不符.
,与题设不符.
当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
因为![]() ,
,![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
从而直线![]() 的方程:
的方程:![]() , ①
, ①
直线![]() 的方程:
的方程:![]() . ②
. ②
由①②,解得![]() ,所以
,所以![]() .
.
因为点![]() 在椭圆上,由对称性,得
在椭圆上,由对称性,得![]() ,即
,即![]() 或
或![]() .
.
又![]() 在椭圆E上,故
在椭圆E上,故![]() .
.
由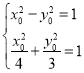 ,解得
,解得![]() ;
;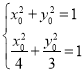 ,无解.
,无解.
因此点P的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn .
(1)求数列{an}的通项公式an及Sn;
(2)若等比数列{bn}的前n项和为Tn , 且b1=2,b4=S4 , 求Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】设O为坐标原点,动点M在椭圆C
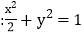 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足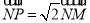
(1) 求点P的轨迹方程;
(2)设点
 在直线x=-3上,且
在直线x=-3上,且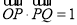 .证明过点P且垂直于OQ的直线l过C的左焦点F.
.证明过点P且垂直于OQ的直线l过C的左焦点F. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
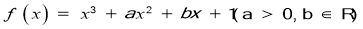 有极值,且导函数
有极值,且导函数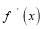 的极值点是
的极值点是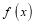 的零点。(极值点是指函数取极值时对应的自变量的值)
的零点。(极值点是指函数取极值时对应的自变量的值)求b关于a的函数关系式,并写出定义域;
证明:b>3a;
若
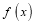 ,
,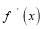 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于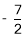 ,求a的取值范围。
,求a的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
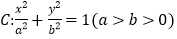 的短轴长为
的短轴长为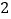 ,椭圆
,椭圆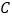 上任意一点到右焦点
上任意一点到右焦点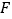 距 离的最大值为
距 离的最大值为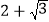 .
.(Ⅰ)求椭圆
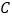 的标准方程;
的标准方程;(Ⅱ)过点
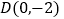 作直线
作直线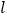 与曲线
与曲线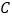 交于
交于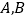 两点,点
两点,点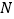 满足
满足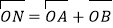 (
(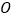 为坐标原点),求四边形
为坐标原点),求四边形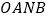 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线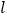 的方程.
的方程. -
科目: 来源: 题型:
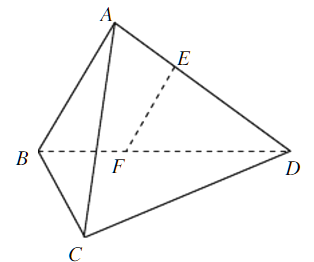
查看答案和解析>>【题目】如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10
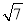 cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.

相关试题

