【题目】已知直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,如图1所示,将
,如图1所示,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,如图2所示.
的位置,如图2所示.
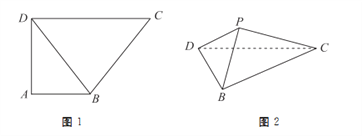
(1)当平面![]() 平面
平面![]() 时,求三棱锥
时,求三棱锥![]() 的体积;
的体积;
(2)在图2中, ![]() 为
为![]() 的中点,若线段
的中点,若线段![]() ,且
,且![]() 平面
平面![]() ,求线段
,求线段![]() 的长;
的长;
参考答案:
【答案】(1)![]() (2)1
(2)1
【解析】试题分析:(1)由面面垂直性质定理得![]() 平面
平面![]() ,即为三棱锥
,即为三棱锥![]() 的高,再根据三棱锥体积公式求体积(2)取
的高,再根据三棱锥体积公式求体积(2)取![]() 的中点
的中点![]() ,则根据三角形中位线性质得
,则根据三角形中位线性质得![]() ,即得
,即得![]() ,再根据线面平行性质定理得
,再根据线面平行性质定理得![]() .即得四边形
.即得四边形![]() 是平行四边形.可得
是平行四边形.可得![]() .
.
试题解析:(1)当平面![]() 平面
平面![]() 时,因为
时,因为![]() ,且平面
,且平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() .因为在直角梯形
.因为在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() .所以
.所以![]() .又因为
.又因为![]() ,所以
,所以![]() ,所以
,所以![]() .所以
.所以![]() .所以三棱锥
.所以三棱锥![]() 的体积等于
的体积等于![]() .
.
 (2)取
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,如上图所示.又因为
,如上图所示.又因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ,且
,且![]() .又因为
.又因为![]() ,所以
,所以![]() .所以
.所以![]() ,
, ![]() ,
, ![]() ,
, ![]() 共面.因为
共面.因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,所以
,所以![]() .又因为
.又因为![]() ,所以四边形
,所以四边形![]() 是平行四边形.所以
是平行四边形.所以![]() .
.
点睛: 将平面图形沿其中一条或几条线段折起,使其成为空间图形,把这类问题称为平面图形的翻折问题.平面图形经过翻折成为空间图形后,原有的性质有的发生了变化,有的没有发生变化,弄清它们是解决问题的关键.一般地,翻折后还在同一个平面上的性质不发生变化,不在同一个平面上的性质发生变化.解决这类问题就是要据此研究翻折以后的空间图形中的线面关系和几何量的度量值,这是化解翻折问题难点的主要方法.立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
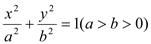 的左、右焦点
的左、右焦点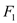 ,
,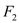 ,离心率
,离心率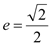 ,短轴长为2.
,短轴长为2.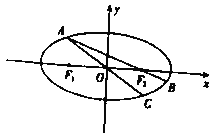
(Ⅰ)求椭圆的方程;
(Ⅱ)如图,点
 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),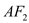 的延长线于椭圆交于
的延长线于椭圆交于 点,
点,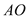 的延长线于椭圆交于
的延长线于椭圆交于 点,求
点,求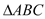 面积的最大值
面积的最大值 -
科目: 来源: 题型:
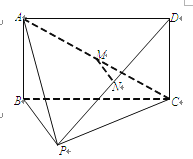
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M为AC的中点,N为PD上一点.
(1)若MN∥平面ABP,求证:N为PD的中点;
(2)若平面ABP⊥平面APC,求证:PC⊥平面ABP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
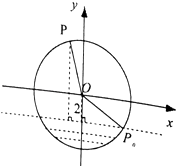
(1)将点P距离水面的高度y(m)与时间t(s)满足的函数关系;
(2)求点P第一次到达最高点需要的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
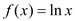 ,
, .
.(Ⅰ)若
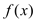 与
与 在
在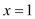 处相切,试求
处相切,试求 的表达式;
的表达式;(Ⅱ)若
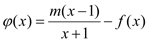 在
在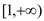 上是减函数,求实数
上是减函数,求实数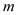 的取值范围;
的取值范围;(Ⅲ)证明不等式:
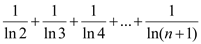
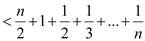 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人约定在中午12时到下午1时之间到某站乘公共汽车,又知这段时间内有4班公共汽车.设到站时间分别为12:15,12:30,12:45,1:00.如果他们约定:
①见车就乘;
②最多等一辆.
试分别求出在两种情况下两人同乘一辆车的概率.假设甲乙两人到达车站的时间是相互独立的,且每人在中午12点到1点的任意时刻到达车站是等可能的. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:不等式(m-1)x2+(m-1)x+2>0的解集是R,命题q:sin x+cos x>m.如果对于任意的x∈R,命题p是真命题且命题q为假命题,求m的范围.
相关试题

