【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() ,离心率
,离心率![]() ,短轴长为2.
,短轴长为2.
(Ⅰ)求椭圆的方程;
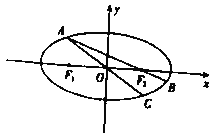
(Ⅱ)如图,点![]() 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),![]() 的延长线于椭圆交于
的延长线于椭圆交于![]() 点,
点,![]() 的延长线于椭圆交于
的延长线于椭圆交于![]() 点,求
点,求![]() 面积的最大值
面积的最大值
参考答案:
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】【试题分析】(1)依据题设建立方程组进行求解;(2)依据题设条件运用直线与椭圆的位置关系建立三角形面积的目标函数,运用不等式求得其最值从而使得问题获解。
(1)椭圆![]() 中,
中,
过其中两个端点的直线斜率为![]() ,∴
,∴![]() ①,
①,
过两个焦点和一个顶点的三角形面积为1,∴![]() ②;
②;
又![]() ③,
③,
用①②③解得![]() ,
,![]() ;
;
∴椭圆的方程为![]() .
.
(2)当直线![]() 的斜率不存在时,
的斜率不存在时,
可知![]() ,
,![]() ,
,![]() ,
,
故![]() ,
,
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
联立方程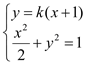 化简得,
化简得,
![]() ,
,
∴![]() ,
,![]() ,
,
故![]() ,
,
![]() ,
,
故![]()
![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离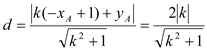 ,
,
故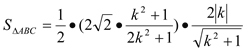
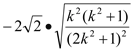
![]()
![]() ;
;
综上,![]() 的面积的最大值为
的面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=
 (弦×矢+矢2).弧田,由圆弧和其所对弦所围成.公式中“弦”指圆弧对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与实际面积之间存在误差.现有圆心角为
(弦×矢+矢2).弧田,由圆弧和其所对弦所围成.公式中“弦”指圆弧对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与实际面积之间存在误差.现有圆心角为  π,弦长等于9米的弧田.按照《九章算术》中弧田面积的经验公式计算所得弧田面积与实际面积的差为 .
π,弦长等于9米的弧田.按照《九章算术》中弧田面积的经验公式计算所得弧田面积与实际面积的差为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
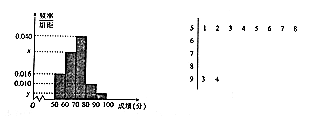
(1)求样本容量n和频率分布直方图中的x,y的值;
(2)估计本次竞赛学生成绩的中位数和平均分;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在[90,100]内的频率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图几何体中,矩形
 所在平面与梯形
所在平面与梯形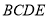 所在平面垂直,且
所在平面垂直,且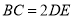 ,
, 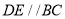 ,
,  ,
, 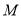 为
为 的中点.
的中点.(1)证明:
 平面
平面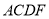 ;
;(2)证明:
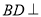 平面
平面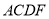 .
.
-
科目: 来源: 题型:
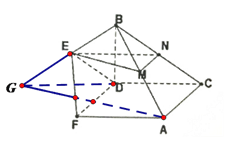
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M为AC的中点,N为PD上一点.
(1)若MN∥平面ABP,求证:N为PD的中点;
(2)若平面ABP⊥平面APC,求证:PC⊥平面ABP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
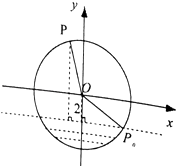
(1)将点P距离水面的高度y(m)与时间t(s)满足的函数关系;
(2)求点P第一次到达最高点需要的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角梯形
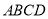 中,
中, 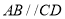 ,
, 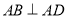 ,
, 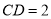 ,
, 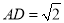 ,
, 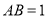 ,如图1所示,将
,如图1所示,将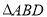 沿
沿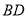 折起到
折起到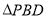 的位置,如图2所示.
的位置,如图2所示.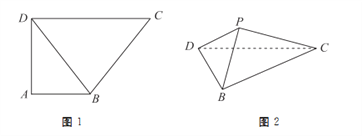
(1)当平面
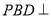 平面
平面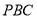 时,求三棱锥
时,求三棱锥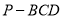 的体积;
的体积;(2)在图2中,
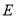 为
为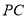 的中点,若线段
的中点,若线段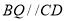 ,且
,且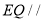 平面
平面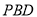 ,求线段
,求线段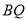 的长;
的长;
相关试题

