【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 与
与![]() 在
在![]() 处相切,试求
处相切,试求![]() 的表达式;
的表达式;
(Ⅱ)若![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)证明不等式:![]()
![]() .
.
参考答案:
【答案】(1)![]() ; (2)
; (2)![]() ;(3)见解析.
;(3)见解析.
【解析】【试题分析】(1)依据题设导数计算公式及导数的几何意义建立方程求解;(2)依据题设条件构造函数运用导数建立不等式,分离参数借助基本不等式求得参数的取值范围;(3)借助(2)的结论建立递推式,然后运用叠加的方法进行分析推证:
(Ⅰ)由于![]() 与
与![]() 在
在![]() 处相切,
处相切,
且![]() ,
,![]() 得:
得:![]()
又∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
(Ⅱ)![]()
![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() 在
在![]() 上恒成立.
上恒成立.
即![]() 在
在![]() 上恒成立,由
上恒成立,由![]() ,
,![]() ,
,
又∵![]() ,∴
,∴![]() 得
得![]() .
.
(Ⅲ)由(Ⅱ)可得:当![]() 时:
时:![]()
![]() 在
在![]() 上是减函数,
上是减函数,
∴当![]() 时,
时,![]() 即
即![]()
![]() ,
,
所以![]() 从而得到:
从而得到:![]() .
.
当![]() 时:
时:![]() ,
,
当![]() 时:
时:![]() ,
,
当![]() 时:
时:![]() ,
,
当![]() 时:
时:![]() ,
,![]() ,
,![]() .
.
上述不等式相加得:
![]()
![]()
![]()
![]()
![]()
![]() …+
…+![]()
![]()
![]()
![]()
即![]()
![]()
![]()
![]()
![]()
![]() …+
…+![]()
![]() .(
.(![]() ,
,![]() )
)
-
科目: 来源: 题型:
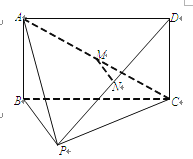
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M为AC的中点,N为PD上一点.
(1)若MN∥平面ABP,求证:N为PD的中点;
(2)若平面ABP⊥平面APC,求证:PC⊥平面ABP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
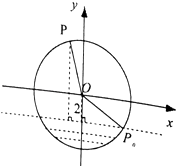
(1)将点P距离水面的高度y(m)与时间t(s)满足的函数关系;
(2)求点P第一次到达最高点需要的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角梯形
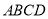 中,
中, 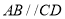 ,
, 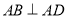 ,
, 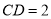 ,
, 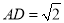 ,
, 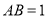 ,如图1所示,将
,如图1所示,将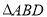 沿
沿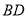 折起到
折起到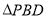 的位置,如图2所示.
的位置,如图2所示.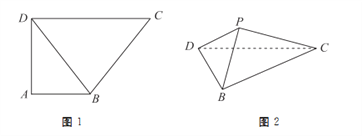
(1)当平面
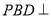 平面
平面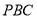 时,求三棱锥
时,求三棱锥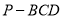 的体积;
的体积;(2)在图2中,
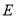 为
为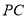 的中点,若线段
的中点,若线段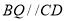 ,且
,且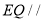 平面
平面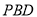 ,求线段
,求线段 的长;
的长; -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人约定在中午12时到下午1时之间到某站乘公共汽车,又知这段时间内有4班公共汽车.设到站时间分别为12:15,12:30,12:45,1:00.如果他们约定:
①见车就乘;
②最多等一辆.
试分别求出在两种情况下两人同乘一辆车的概率.假设甲乙两人到达车站的时间是相互独立的,且每人在中午12点到1点的任意时刻到达车站是等可能的. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:不等式(m-1)x2+(m-1)x+2>0的解集是R,命题q:sin x+cos x>m.如果对于任意的x∈R,命题p是真命题且命题q为假命题,求m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
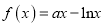 ,
, 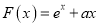 ,其中
,其中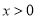 ,
, 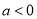 ,
,  为自然对数的底数.
为自然对数的底数. (Ⅰ)若
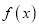 和
和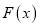 在区间
在区间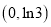 内具有相同的单调性,求实数
内具有相同的单调性,求实数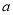 的取值范围;
的取值范围;(Ⅱ)若
 ,且函数
,且函数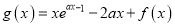 的最小值为
的最小值为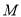 ,求
,求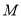 的最小值.
的最小值.
相关试题

