【题目】已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有 ![]() ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
A.0<a≤5
B.a<5
C.0<a<5
D.a≥5
参考答案:
【答案】A
【解析】解:∵定义域为(0,+∞)的单调函数f(x) 满足f[f(x)+ ![]() x]=4,
x]=4,
∴必存在唯一的正实数a,
满足f(x)+ ![]() x=a,f(a)=4,①
x=a,f(a)=4,①
∴f(a)+ ![]() a=a,②
a=a,②
由①②得:4+ ![]() a=a,
a=a, ![]() a=a﹣4,
a=a﹣4,
a=( ![]() )a﹣4 , 左增,右减,有唯一解a=3,
)a﹣4 , 左增,右减,有唯一解a=3,
故f(x)+ ![]() x=a=3,
x=a=3,
f(x)=3﹣ ![]() x,
x,
由方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,
即有| ![]() x|=x3﹣6x2+9x﹣4+a,
x|=x3﹣6x2+9x﹣4+a,
由g(x)=x3﹣6x2+9x﹣4+a,g′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3),
当1<x<3时,g′(x)<0,g(x)递减;当0<x<1时,g′(x)<0,g(x)递增.
g(x)在x=1处取得最大值a,g(0)=a﹣4,g(3)=a﹣4,
分别作出y=| ![]() x|,和y=x3﹣6x2+9x﹣4的图象,可得
x|,和y=x3﹣6x2+9x﹣4的图象,可得
两图象只有一个交点,将y=x3﹣6x2+9x﹣4的图象向上平移,
至经过点(3,1),有两个交点,
由g(3)=1即a﹣4=1,解得a=5,
当0<a≤5时,两图象有两个交点,
即方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解.
故选:A.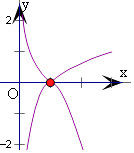
由题设知必存在唯一的正实数a,满足f(x)+ ![]() x=a,f(a)=4,f(a)+
x=a,f(a)=4,f(a)+ ![]() a=a,故4+
a=a,故4+ ![]() a=a,
a=a, ![]() a=a﹣4,a=(
a=a﹣4,a=( ![]() )a﹣4 , 左增,右减,有唯一解a=3,故f(x)+
)a﹣4 , 左增,右减,有唯一解a=3,故f(x)+ ![]() x=a=3,由题意可得|
x=a=3,由题意可得| ![]() x|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,讨论g(x)=x3﹣6x2+9x﹣4+a的单调性和最值,分别画出作出y=|
x|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,讨论g(x)=x3﹣6x2+9x﹣4+a的单调性和最值,分别画出作出y=| ![]() x|,和y=x3﹣6x2+9x﹣4的图象,通过平移即可得到a的范围.
x|,和y=x3﹣6x2+9x﹣4的图象,通过平移即可得到a的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某项“过关游戏”规则规定:在地
 关要抛掷
关要抛掷 颗骰子
颗骰子 次,如果这
次,如果这 次抛掷所出现的点数和大于
次抛掷所出现的点数和大于 ,则算过关.
,则算过关.(Ⅰ)此游戏最多能过__________关.
(Ⅱ)连续通过第
 关、第
关、第 关的概率是__________.
关的概率是__________.(Ⅲ)若直接挑战第
 关,则通关的概率是__________.
关,则通关的概率是__________.(Ⅳ)若直接挑战第
 关,则通关的概率是__________.
关,则通关的概率是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
-
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,如果输出T=6,那么判断框内应填入的条件是( )
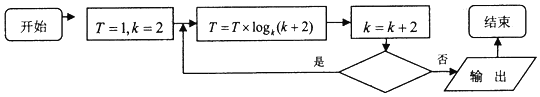
A.k<32
B.k<33
C.k<64
D.k<65 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经销某商品,顾客可以采用一次性付款或分期付款购买,根据以往资料统计,顾客采用一次性付款的概率是
 ,经销
,经销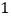 件该产品,若顾客采用一次性付款,商场获得利润
件该产品,若顾客采用一次性付款,商场获得利润 元;若顾客采用分期付款,商场获得利润
元;若顾客采用分期付款,商场获得利润 元.
元.(Ⅰ)求
 位购买商品的顾客中至少有
位购买商品的顾客中至少有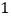 位采用一次性付款的概率.
位采用一次性付款的概率.(Ⅱ)若
 位顾客每人购买
位顾客每人购买 件该商品,求商场获得利润不超过
件该商品,求商场获得利润不超过 元的概率.
元的概率.(Ⅲ)若
 位顾客每人购买
位顾客每人购买 件该商品,设商场获得的利润为随机变量
件该商品,设商场获得的利润为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC外接圆半径是2,
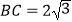 ,则△ABC的面积最大值为
,则△ABC的面积最大值为 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, 和
和 是函数
是函数 的图象与
的图象与 轴的
轴的 个相邻交点的横坐标,且当
个相邻交点的横坐标,且当 时,
时, 取得最大值
取得最大值 .
.(1)求数
 的表达式;
的表达式;(2)将函数
 的图象上的每一点的横坐标变为原来的
的图象上的每一点的横坐标变为原来的 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象,再将函数
的图象,再将函数 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象.
的图象.①求函数
 的解析式;
的解析式;②求函数
 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
相关试题

