【题目】已知△ABC外接圆半径是2, ![]() ,则△ABC的面积最大值为
,则△ABC的面积最大值为
参考答案:
【答案】![]()
【解析】解:∵△ABC外接圆半径是2, ![]() , ∴由正弦定理
, ∴由正弦定理 ![]() ,可得:
,可得: ![]() =2×2,解得:sinA=
=2×2,解得:sinA= ![]() ,
,
∵A∈(0,π),
∴A= ![]() ,或
,或 ![]() ,
,
∴当A= ![]() 时,由余弦定理可得:
时,由余弦定理可得:
12=AB2+AC2﹣2ABACcosA=AB2+AC2﹣ABAC≥ABAC,
此时S△ABC= ![]() ABACsinA≤
ABACsinA≤ ![]() =3
=3 ![]() .
.
当A= ![]() 时,由余弦定理可得:12=AB2+AC2﹣2ABACcosA=AB2+AC2+ABAC≥3ABAC,
时,由余弦定理可得:12=AB2+AC2﹣2ABACcosA=AB2+AC2+ABAC≥3ABAC,
解得:4≥ABAC,此时S△ABC= ![]() ABACsinA≤
ABACsinA≤ ![]() =
= ![]() .
.
∴△ABC的面积最大值为3 ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用正弦定理的定义对题目进行判断即可得到答案,需要熟知正弦定理:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,如果输出T=6,那么判断框内应填入的条件是( )
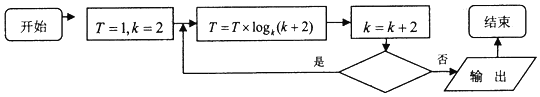
A.k<32
B.k<33
C.k<64
D.k<65 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有
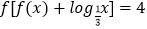 ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
A.0<a≤5
B.a<5
C.0<a<5
D.a≥5 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经销某商品,顾客可以采用一次性付款或分期付款购买,根据以往资料统计,顾客采用一次性付款的概率是
 ,经销
,经销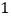 件该产品,若顾客采用一次性付款,商场获得利润
件该产品,若顾客采用一次性付款,商场获得利润 元;若顾客采用分期付款,商场获得利润
元;若顾客采用分期付款,商场获得利润 元.
元.(Ⅰ)求
 位购买商品的顾客中至少有
位购买商品的顾客中至少有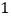 位采用一次性付款的概率.
位采用一次性付款的概率.(Ⅱ)若
 位顾客每人购买
位顾客每人购买 件该商品,求商场获得利润不超过
件该商品,求商场获得利润不超过 元的概率.
元的概率.(Ⅲ)若
 位顾客每人购买
位顾客每人购买 件该商品,设商场获得的利润为随机变量
件该商品,设商场获得的利润为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, 和
和 是函数
是函数 的图象与
的图象与 轴的
轴的 个相邻交点的横坐标,且当
个相邻交点的横坐标,且当 时,
时, 取得最大值
取得最大值 .
.(1)求数
 的表达式;
的表达式;(2)将函数
 的图象上的每一点的横坐标变为原来的
的图象上的每一点的横坐标变为原来的 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象,再将函数
的图象,再将函数 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象.
的图象.①求函数
 的解析式;
的解析式;②求函数
 在区间
在区间 上的最大值和最小值.
上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
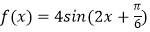 (
( 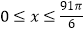 ),若函数F(x)=f(x)﹣3的所有零点依次记为x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 则x1+2x2+2x3+…+2xn﹣1+xn= .
),若函数F(x)=f(x)﹣3的所有零点依次记为x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 则x1+2x2+2x3+…+2xn﹣1+xn= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知公比不为1的等比数列{an}的前5项积为243,且2a3为3a2和a4的等差中项.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=bn﹣1log3an+2(n≥2且n∈N*),且b1=1,求数列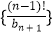 的前n项和Sn .
的前n项和Sn .
相关试题

