【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
, ![]() 的值;
的值;
(2)当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() ,
, ![]() ;(2) 实数
;(2) 实数![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:(1)求出![]() ,由
,由![]() ,
, ![]() 可求得
可求得![]() ,
, ![]() 的值;(2)
的值;(2)![]() 恒成立等价于
恒成立等价于![]() . 设
. 设![]() ,利用导数研究函数的单调性,讨论可证明证明当
,利用导数研究函数的单调性,讨论可证明证明当![]() 时,
时, ![]() 恒成立,当
恒成立,当![]() 时,不合题意,从而可得结果.
时,不合题意,从而可得结果.
试题解析:(1)函![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
把![]() 代入方程
代入方程![]() 中,得
中,得![]() ,
,
即![]() ,∴
,∴![]() ,
,
又因为![]() ,∴
,∴![]() ,
,
故![]() .
.
(2)由(1)可知![]() ,当
,当![]() 时,
时,
![]() 恒成立等价于
恒成立等价于![]() .
.
设![]() ,
,
则![]()
![]() ,
,
由于![]() ,
,
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
![]() 恒成立.
恒成立.
当![]() 时,设
时,设![]() ,则
,则![]() .
.
则![]() 为
为![]() 上单调递增函数,
上单调递增函数,
又由![]() .
.
即![]() 在
在![]() 上存在
上存在![]() ,使得
,使得![]() ,
,
当![]() 时,
时, ![]() 单调递减,
单调递减,
当![]() 时,
时, ![]() 单调递增;
单调递增;
则![]() ,不合题意,舍去.
,不合题意,舍去.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家电公司根据销售区域将销售员分成
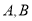 两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间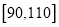 内,将这些数据分成4组:
内,将这些数据分成4组: 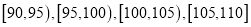 ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:
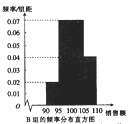
以上面数据的频率作为概率,分别从
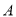 组与
组与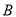 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记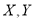 分别表示
分别表示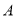 组与
组与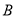 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.(1)求
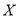 的分布列及数学期;
的分布列及数学期;(2)试问
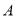 组与
组与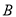 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】某海产品经销商调查发现,该海产品每售出
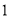 吨可获利
吨可获利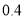 万元,每积压
万元,每积压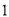 吨则亏损
吨则亏损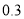 万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.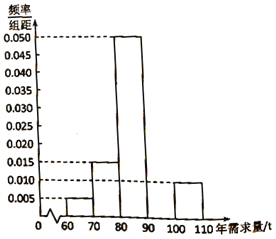
(1)请补齐
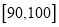 上的频率分布直方图,并依据该图估计年需求量的平均数;
上的频率分布直方图,并依据该图估计年需求量的平均数;(2)今年该经销商欲进货
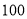 吨,以
吨,以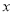 (单位:吨,
(单位:吨, 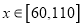 )表示今年的年需求量,以
)表示今年的年需求量,以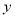 (单位:万元)表示今年销售的利润,试将
(单位:万元)表示今年销售的利润,试将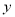 表示为
表示为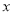 的函数解析式;并求今年的年利润不少于
的函数解析式;并求今年的年利润不少于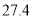 万元的概率.
万元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
:  的焦点为
的焦点为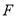 ,圆
,圆 :
:  ,过
,过 作垂直于
作垂直于 轴的直线交抛物线
轴的直线交抛物线 于
于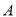 、
、 两点,且
两点,且 的面积为
的面积为 .
.(1)求抛物线
 的方程和圆
的方程和圆 的方程;
的方程;(2)若直线
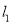 、
、 均过坐标原点
均过坐标原点 ,且互相垂直,
,且互相垂直,  交抛物线
交抛物线 于
于 ,交圆
,交圆 于
于 ,
,  交抛物线
交抛物线 于
于 ,交圆
,交圆 于
于 ,求
,求 与
与 的面积比的最小值.
的面积比的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥
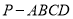 ,
, 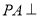 平面
平面 ,底面
,底面 中,
中, 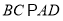 ,
,  ,且
,且 ,
,  为
为 的中点.
的中点.
(1)求证:平面
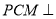 平面
平面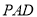 ;
;(2)问在棱
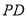 上是否存在点
上是否存在点 ,使
,使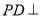 平面
平面 ,若存在,请求出二面角
,若存在,请求出二面角 的余弦值;若不存在,请说明理由.
的余弦值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某省高中男生身高统计调查数据显示:全省
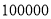 名男生的身高服从正态分布
名男生的身高服从正态分布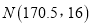 ,现从该生某校高三年级男生中随机抽取
,现从该生某校高三年级男生中随机抽取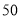 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于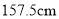 和
和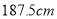 之间,将测量结果按如下方式分成
之间,将测量结果按如下方式分成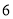 组:第一组
组:第一组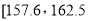 ,第二组
,第二组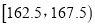 ,…,第六组
,…,第六组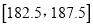 ,下图是按照上述分组方法得到的频率分布直方图.
,下图是按照上述分组方法得到的频率分布直方图.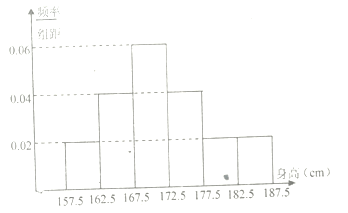
(1)求该学校高三年级男生的平均身高;
(2)求这
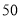 名男生中身高在
名男生中身高在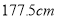 以上(含
以上(含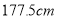 )的人数;
)的人数;(3)从这
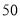 名男生中身高在
名男生中身高在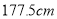 以上(含
以上(含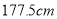 )的人中任意抽取
)的人中任意抽取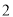 人,该
人,该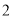 中身高排名(从高到低)在全省前
中身高排名(从高到低)在全省前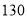 名的人数记为
名的人数记为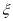 ,求
,求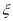 的数学期望.
的数学期望.(附:参考数据:若
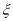 服从正态分布
服从正态分布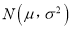 ,则
,则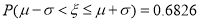 ,
, 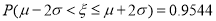 ,
, 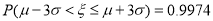 .)
.) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
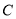 :
: 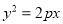 (
(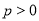 )的焦点是椭圆
)的焦点是椭圆 :
: 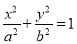 (
(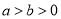 )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点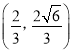
(1)求椭圆
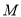 的方程;
的方程;(2)椭圆
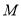 的左、右顶点分别为
的左、右顶点分别为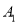 ,
, 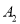 ,若过点
,若过点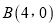 且斜率不为零的直线
且斜率不为零的直线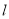 与椭圆
与椭圆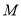 交于
交于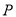 ,
,  两点,已知直线
两点,已知直线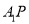 与
与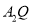 相较于点
相较于点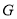 ,试判断点
,试判断点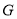 是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
相关试题

