【题目】已知抛物线![]() :
: ![]() (
(![]() )的焦点是椭圆
)的焦点是椭圆![]() :
: ![]() (
(![]() )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点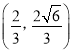
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
, ![]() ,若过点
,若过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,已知直线
两点,已知直线![]() 与
与![]() 相较于点
相较于点![]() ,试判断点
,试判断点![]() 是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
参考答案:
【答案】(1) ![]() (2) 点
(2) 点![]() 在定直线
在定直线![]() 上
上
【解析】试题分析:(1)由条件易得: 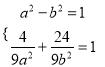 ,从而得到椭圆
,从而得到椭圆![]() 的方程;
的方程;
(2)先由特殊位置定出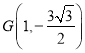 ,猜想点
,猜想点![]() 在直线
在直线![]() 上,由条件可得直线
上,由条件可得直线![]() 的斜率存在, 设直线
的斜率存在, 设直线![]() ,联立方程
,联立方程![]() ,消
,消![]() 得:
得: ![]() 有两个不等的实根,利用韦达定理转化条件即可.
有两个不等的实根,利用韦达定理转化条件即可.
试题解析:
(1)将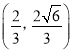 代入抛物线
代入抛物线![]() 得
得![]()
∴抛物线的焦点为![]() ,则椭圆
,则椭圆![]() 中
中![]() ,
,
又点 在椭圆
在椭圆![]() 上,
上,
∴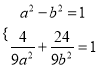 , 解得
, 解得![]() ,
,
椭圆![]() 的方程为
的方程为![]()
(2)方法一
当点![]() 为椭圆的上顶点时,直线img src="http://thumb.zyjl.cn/questionBank/Upload/2018/08/07/18/5075df16/SYS201808071806350814512596_DA/SYS201808071806350814512596_DA.027.png" width="9" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的方程为
为椭圆的上顶点时,直线img src="http://thumb.zyjl.cn/questionBank/Upload/2018/08/07/18/5075df16/SYS201808071806350814512596_DA/SYS201808071806350814512596_DA.027.png" width="9" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的方程为![]() ,此时点
,此时点![]() ,
, 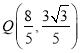 ,则直线
,则直线![]() 和直线
和直线![]() ,联立
,联立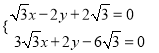 ,解得
,解得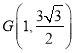 ,
,
当点![]() 为椭圆的下顶点时,由对称性知:
为椭圆的下顶点时,由对称性知: 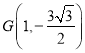 .
.
猜想点![]() 在直线
在直线![]() 上,证明如下:
上,证明如下:
由条件可得直线![]() 的斜率存在, 设直线
的斜率存在, 设直线![]() ,
,
联立方程![]() ,
,
消![]() 得:
得: ![]() 有两个不等的实根,
有两个不等的实根,
![]() ,
, ![]()
设![]() ,则
,则![]() ,
, ![]()
则直线![]() 与直线
与直线![]()
联立两直线方程得![]() (其中
(其中![]() 为
为![]() 点横坐标)
点横坐标)
将![]() 代入上述方程中可得
代入上述方程中可得![]() ,
,
即![]() ,
,
即证![]()
将![]() 代入上式可得
代入上式可得![]()
![]() ,此式成立
,此式成立
∴点![]() 在定直线
在定直线![]() 上.
上.
方法二
由条件可得直线![]() 的斜率存在, 设直线
的斜率存在, 设直线![]()
联立方程![]() ,
,
消![]() 得:
得: ![]() 有两个不等的实根,
有两个不等的实根,
![]() ,
, ![]()
设![]() ,则
,则![]() ,
, ![]()
![]() ,
,
由![]() ,
, ![]() ,
, ![]() 三点共线,有:
三点共线,有: ![]()
由![]() ,
, ![]() ,
, ![]() 三点共线,有:
三点共线,有: ![]()
上两式相比得![]()
![]() ,
,
解得![]()
∴点![]() 在定直线
在定直线![]() 上.
上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
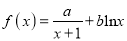 ,曲线
,曲线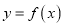 在点
在点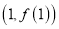 处的切线方程为
处的切线方程为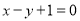 .
.(1)求
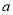 ,
, 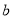 的值;
的值;(2)当
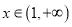 时,
时, 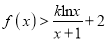 恒成立,求实数
恒成立,求实数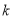 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥
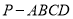 ,
, 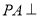 平面
平面 ,底面
,底面 中,
中, 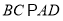 ,
,  ,且
,且 ,
,  为
为 的中点.
的中点.
(1)求证:平面
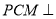 平面
平面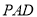 ;
;(2)问在棱
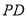 上是否存在点
上是否存在点 ,使
,使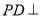 平面
平面 ,若存在,请求出二面角
,若存在,请求出二面角 的余弦值;若不存在,请说明理由.
的余弦值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某省高中男生身高统计调查数据显示:全省
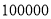 名男生的身高服从正态分布
名男生的身高服从正态分布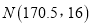 ,现从该生某校高三年级男生中随机抽取
,现从该生某校高三年级男生中随机抽取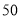 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于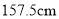 和
和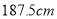 之间,将测量结果按如下方式分成
之间,将测量结果按如下方式分成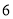 组:第一组
组:第一组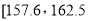 ,第二组
,第二组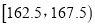 ,…,第六组
,…,第六组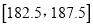 ,下图是按照上述分组方法得到的频率分布直方图.
,下图是按照上述分组方法得到的频率分布直方图.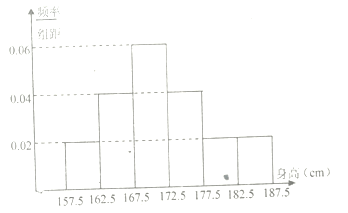
(1)求该学校高三年级男生的平均身高;
(2)求这
 名男生中身高在
名男生中身高在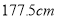 以上(含
以上(含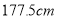 )的人数;
)的人数;(3)从这
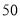 名男生中身高在
名男生中身高在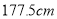 以上(含
以上(含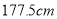 )的人中任意抽取
)的人中任意抽取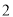 人,该
人,该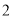 中身高排名(从高到低)在全省前
中身高排名(从高到低)在全省前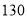 名的人数记为
名的人数记为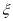 ,求
,求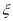 的数学期望.
的数学期望.(附:参考数据:若
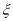 服从正态分布
服从正态分布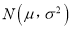 ,则
,则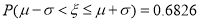 ,
, 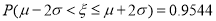 ,
, 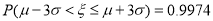 .)
.) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
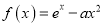 ,
, 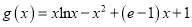 ,且曲线
,且曲线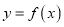 在
在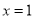 处的切线方程为
处的切线方程为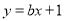 .
.(1)求
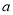 ,
, 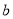 的值;
的值;(2)求函数
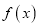 在
在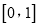 上的最小值;
上的最小值;(3)证明:当
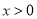 时,
时, 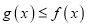 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直角坐标系中动点
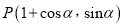 ,参数
,参数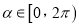 ,在以原点为极点、
,在以原点为极点、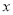 轴正半轴为极轴所建立的极坐标系中,动点
轴正半轴为极轴所建立的极坐标系中,动点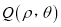 在曲线
在曲线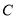 :
: 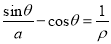 上.
上.(1)求点
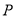 的轨迹
的轨迹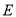 的普通方程和曲线
的普通方程和曲线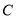 的直角坐标方程;
的直角坐标方程;(2)若动点
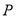 的轨迹
的轨迹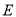 和曲线
和曲线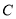 有两个公共点,求实数
有两个公共点,求实数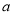 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】现在的人基本每天都离不开手机,许多人手机一旦不在身边就不舒服,几乎达到手机二十四小时不离身,这类人群被称为“手机控”,这一群体在大学生中比较突出.为了调查大学生每天使用手机的时间,某调查公司针对某高校男生、女生各25名学生进行了调查,其中每天使用手机时间超过8小时的被称为:“手机控”,否则被称为“非手机控”.调查结果如下:
手机控
非手机控
合计
女生
5
男生
10
合计
50
(1)将上面的列联表补充完整,再判断是否有99.5%的把握认为“手机控”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“手机控”的人数为
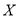 ,试求
,试求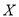 的分布列与数学期望.
的分布列与数学期望.参考公式:
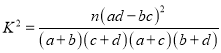 ,其中
,其中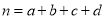 .
.
相关试题

