【题目】如图,已知四棱锥![]() ,
, ![]() 平面
平面![]() ,底面
,底面![]() 中,
中, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)问在棱![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,请求出二面角
,若存在,请求出二面角![]() 的余弦值;若不存在,请说明理由.
的余弦值;若不存在,请说明理由.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)要证平面![]() 平面
平面![]() ,即证
,即证![]() 平面
平面![]() ,即证:
,即证: ![]()
(2) 存在点![]() 使
使![]() 平面
平面![]() ,在
,在![]() 内,过
内,过![]() 做
做![]() 垂足为
垂足为![]() ,易知
,易知![]() 为二面角
为二面角![]() 的平面角,从而得到结果.
的平面角,从而得到结果.
试题解析:
方法一:(1)证明:∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() . ∵
. ∵![]() 为
为![]() 的中点,且梯形
的中点,且梯形![]() 中
中![]() ,
, ![]() ,
,
∴![]()
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,且
,且![]()
∴![]() 平面
平面![]() .
.
![]() 平面
平面![]() , ∴平面
, ∴平面![]() ⊥平面
⊥平面![]()
(2)存在点![]() 使
使![]() 平面
平面![]() ,在
,在![]() 内,过
内,过![]() 做
做![]() 垂足为
垂足为![]()
由(1)![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
![]() ,
, ![]() 平面
平面![]()
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 知
知 ![]() ,
, ![]()
∵平面![]() 平面
平面![]()
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
故二面角![]() 的余弦值为
的余弦值为![]() .
.
方法二:
∴以![]() 为原点,射线
为原点,射线![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 轴的正半轴,建立空间直角坐标系如图
轴的正半轴,建立空间直角坐标系如图
![]() ,
,
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
, ![]()
(1)![]()
∴![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,且
,且![]()
∴![]() 平面
平面![]() .
.
![]() 平面
平面![]() , ∴平面
, ∴平面![]() ⊥平面
⊥平面![]()
(2)存在点![]() 使
使![]() 平面
平面![]() ,在
,在![]() 内,过
内,过![]() 做
做![]() 垂足为
垂足为![]()
由(1)![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,

![]() ,
, ![]() 平面
平面![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() ,
,
![]() ,
,
取![]() .
.
![]()
![]() 平面
平面![]()
![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
由图形知二面角![]() 的平面角
的平面角![]() 是锐角,
是锐角,
故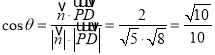
所以二面角余弦值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某海产品经销商调查发现,该海产品每售出
 吨可获利
吨可获利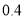 万元,每积压
万元,每积压 吨则亏损
吨则亏损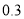 万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.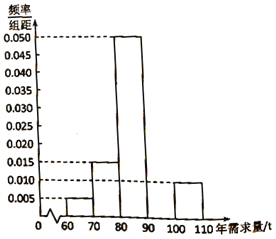
(1)请补齐
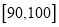 上的频率分布直方图,并依据该图估计年需求量的平均数;
上的频率分布直方图,并依据该图估计年需求量的平均数;(2)今年该经销商欲进货
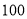 吨,以
吨,以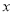 (单位:吨,
(单位:吨, 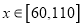 )表示今年的年需求量,以
)表示今年的年需求量,以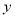 (单位:万元)表示今年销售的利润,试将
(单位:万元)表示今年销售的利润,试将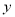 表示为
表示为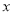 的函数解析式;并求今年的年利润不少于
的函数解析式;并求今年的年利润不少于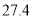 万元的概率.
万元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
:  的焦点为
的焦点为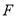 ,圆
,圆 :
:  ,过
,过 作垂直于
作垂直于 轴的直线交抛物线
轴的直线交抛物线 于
于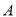 、
、 两点,且
两点,且 的面积为
的面积为 .
.(1)求抛物线
 的方程和圆
的方程和圆 的方程;
的方程;(2)若直线
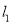 、
、 均过坐标原点
均过坐标原点 ,且互相垂直,
,且互相垂直,  交抛物线
交抛物线 于
于 ,交圆
,交圆 于
于 ,
,  交抛物线
交抛物线 于
于 ,交圆
,交圆 于
于 ,求
,求 与
与 的面积比的最小值.
的面积比的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
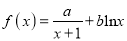 ,曲线
,曲线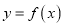 在点
在点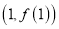 处的切线方程为
处的切线方程为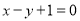 .
.(1)求
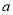 ,
, 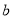 的值;
的值;(2)当
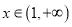 时,
时, 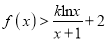 恒成立,求实数
恒成立,求实数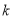 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某省高中男生身高统计调查数据显示:全省
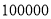 名男生的身高服从正态分布
名男生的身高服从正态分布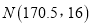 ,现从该生某校高三年级男生中随机抽取
,现从该生某校高三年级男生中随机抽取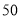 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于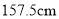 和
和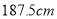 之间,将测量结果按如下方式分成
之间,将测量结果按如下方式分成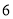 组:第一组
组:第一组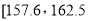 ,第二组
,第二组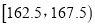 ,…,第六组
,…,第六组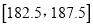 ,下图是按照上述分组方法得到的频率分布直方图.
,下图是按照上述分组方法得到的频率分布直方图.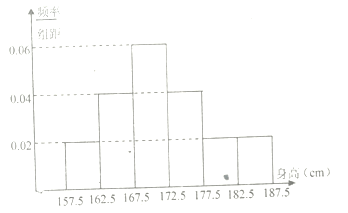
(1)求该学校高三年级男生的平均身高;
(2)求这
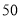 名男生中身高在
名男生中身高在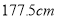 以上(含
以上(含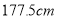 )的人数;
)的人数;(3)从这
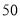 名男生中身高在
名男生中身高在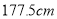 以上(含
以上(含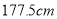 )的人中任意抽取
)的人中任意抽取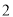 人,该
人,该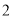 中身高排名(从高到低)在全省前
中身高排名(从高到低)在全省前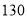 名的人数记为
名的人数记为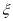 ,求
,求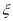 的数学期望.
的数学期望.(附:参考数据:若
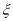 服从正态分布
服从正态分布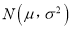 ,则
,则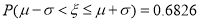 ,
, 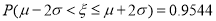 ,
, 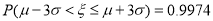 .)
.) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
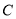 :
: 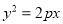 (
(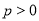 )的焦点是椭圆
)的焦点是椭圆 :
: 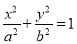 (
(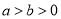 )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点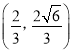
(1)求椭圆
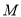 的方程;
的方程;(2)椭圆
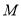 的左、右顶点分别为
的左、右顶点分别为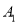 ,
, 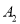 ,若过点
,若过点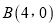 且斜率不为零的直线
且斜率不为零的直线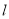 与椭圆
与椭圆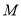 交于
交于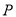 ,
,  两点,已知直线
两点,已知直线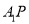 与
与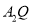 相较于点
相较于点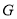 ,试判断点
,试判断点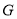 是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
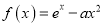 ,
, 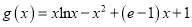 ,且曲线
,且曲线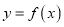 在
在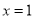 处的切线方程为
处的切线方程为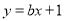 .
.(1)求
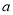 ,
, 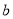 的值;
的值;(2)求函数
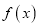 在
在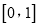 上的最小值;
上的最小值;(3)证明:当
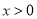 时,
时, 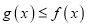 .
.
相关试题

