【题目】已知![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析: (1)求出f(x)的导数,可得切线的斜率,由斜截式方程即可得到所求切线的方程;
(2)由题意可得存在x0∈[0,+∞),使得![]() ,设
,设![]() ,两次求导,判断单调性,对a讨论,分
,两次求导,判断单调性,对a讨论,分![]() 和
和![]() 时,通过构造函数和求导,得到单调区间,可得最值,即可得到所求a的范围.
时,通过构造函数和求导,得到单调区间,可得最值,即可得到所求a的范围.
试题解析:(1)![]() 时,
时, ![]() ,
, ![]()
![]() ,
, ![]() ,
,
所以![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(2)存在![]() ,
, ![]() ,
,
即: ![]() 在
在![]() 时有解;
时有解;
设![]() ,
, ![]()
令![]() ,
, ![]()
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]()
1°当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 单调增,
单调增,
所以![]() ,所以
,所以![]()
2°当![]() 时,
时, ![]()
设![]() ,
,
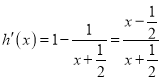
令![]() ,
, ![]()
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
所以![]() ,所以
,所以![]()
所以![]()
![]()
设![]() ,
, ![]() ,
,
令![]() ,
, ![]()
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]()
所以![]() 在
在![]() 单调递增,∴
单调递增,∴![]() ,
,
所以![]() ,
,
所以![]()
所以,当![]() 时,
时, ![]() 恒成立,不合题意
恒成立,不合题意
综上,实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率;
(2)检验结束后,甲、乙两名运动员的成绩如下:
甲:70,68,74,71,72
乙:70,69,70,74,72
根据两组数据完成图示的茎叶图,并通过计算说明哪位运动员的成绩更稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
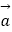 =(
=( 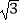 sinx,m+cosx),
sinx,m+cosx),  =(cosx,﹣m+cosx),且f(x)=
=(cosx,﹣m+cosx),且f(x)= 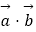
(1)求函数f(x)的解析式;
(2)当x∈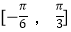 时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2cosxsin(x﹣
 )+
)+  .
.
(1)求函数f(x)的对称轴方程;
(2)若方程sin2x+2|f(x+ )|﹣m+1=0在x∈
)|﹣m+1=0在x∈  上有三个实数解,求实数m的取值范围.
上有三个实数解,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a、b、c分别是角A、B、C的对边,如果a,b,c成等差数列,B=60°,△ABC的面积为3
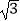 ,那么b等于( )
,那么b等于( )
A.2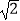
B.2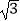
C.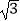
D.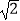
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,其左、右焦点分别为
,其左、右焦点分别为 ,点
,点 是坐标平面内一点,且
是坐标平面内一点,且 ,
,  (
( 为坐标原点).
为坐标原点).(1)求椭圆
 的方程;
的方程;(2)过点
 且斜率为
且斜率为 的动直线
的动直线 交椭圆于
交椭圆于 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以 为直径的圆恒过该点?若存在,求出点
为直径的圆恒过该点?若存在,求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式ax2+bx+c<0的解集为{x|x<﹣2或x>﹣
 },则关于x的不等式ax2﹣bx+c>0的解集为 .
},则关于x的不等式ax2﹣bx+c>0的解集为 .
相关试题

