【题目】在△ABC中,a、b、c分别是角A、B、C的对边,如果a,b,c成等差数列,B=60°,△ABC的面积为3 ![]() ,那么b等于( )
,那么b等于( )
A.2 ![]()
B.2 ![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:在△ABC中,∵a、b、c成等差数列,∴2b=a+c, 又∠B=60°,△ABC的面积为3 ![]() ,
,
∴ ![]() acsinB=
acsinB= ![]() acsin60°=3
acsin60°=3 ![]() ,即
,即 ![]() ×
× ![]() ac=3
ac=3 ![]() ,ac=12.
,ac=12.
由余弦定理b2=a2+c2﹣2accosB,得:
b2=a2+c2﹣2accos60°,即b2=(a+c)2﹣3ac,
∴b2=4b2﹣3×12,
∴b=2 ![]() .
.
故选:B.
由a、b、c成等差数列,把a+c用b表示,由面积等于3 ![]() 求出ac=12,结合余弦定理列式求b的值.
求出ac=12,结合余弦定理列式求b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
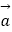 =(
=( 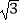 sinx,m+cosx),
sinx,m+cosx),  =(cosx,﹣m+cosx),且f(x)=
=(cosx,﹣m+cosx),且f(x)= 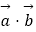
(1)求函数f(x)的解析式;
(2)当x∈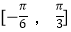 时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2cosxsin(x﹣
 )+
)+  .
.
(1)求函数f(x)的对称轴方程;
(2)若方程sin2x+2|f(x+ )|﹣m+1=0在x∈
)|﹣m+1=0在x∈  上有三个实数解,求实数m的取值范围.
上有三个实数解,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
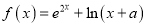 .
.(1)当
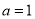 时,求
时,求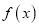 在
在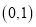 处的切线方程;
处的切线方程;(2)若存在
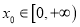 ,使得
,使得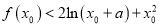 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,其左、右焦点分别为
,其左、右焦点分别为 ,点
,点 是坐标平面内一点,且
是坐标平面内一点,且 ,
,  (
( 为坐标原点).
为坐标原点).(1)求椭圆
 的方程;
的方程;(2)过点
 且斜率为
且斜率为 的动直线
的动直线 交椭圆于
交椭圆于 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以 为直径的圆恒过该点?若存在,求出点
为直径的圆恒过该点?若存在,求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式ax2+bx+c<0的解集为{x|x<﹣2或x>﹣
 },则关于x的不等式ax2﹣bx+c>0的解集为 .
},则关于x的不等式ax2﹣bx+c>0的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程C:x2+y2﹣2x﹣4y+m=0,
(1)若方程C表示圆,求实数m的范围;
(2)在方程表示圆时,该圆与直线l:x+2y﹣4=0相交于M、N两点,且|MN|= ,求m的值.
,求m的值.
相关试题

