【题目】为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率;
(2)检验结束后,甲、乙两名运动员的成绩如下:
甲:70,68,74,71,72
乙:70,69,70,74,72
根据两组数据完成图示的茎叶图,并通过计算说明哪位运动员的成绩更稳定.
参考答案:
【答案】
(1)解:从6人中随机选出2人,选出的2人中至少有1个女运动员的概率为
P=1﹣ ![]() =1﹣
=1﹣ ![]() =
= ![]() ;
;
(2)解:根据题目中的数据,画出茎叶图如图所示;

设甲运动员的平均成绩为 ![]() ,方差为
,方差为 ![]() ,
,
乙运动员的平均成绩为 ![]() ,方差为
,方差为 ![]() ,
,
可得 ![]() =
= ![]() ×(68+70+71+72+74)=71,
×(68+70+71+72+74)=71,
![]() =
= ![]() ×(69+70+70+72+74)=71,
×(69+70+70+72+74)=71,
![]() =
= ![]() ×[(68﹣71)2+(70﹣71)2+(71﹣71)2+(72﹣71)2+(74﹣71)2]=4,
×[(68﹣71)2+(70﹣71)2+(71﹣71)2+(72﹣71)2+(74﹣71)2]=4,
![]() =
= ![]() ×[(69﹣71)2+(70﹣71)2+(70﹣71)2+(72﹣71)2+(74﹣71)2]=3.2.
×[(69﹣71)2+(70﹣71)2+(70﹣71)2+(72﹣71)2+(74﹣71)2]=3.2.
∵ ![]() =
= ![]() ,
, ![]() >
> ![]() ,故乙运动员的成绩更稳定.
,故乙运动员的成绩更稳定.
【解析】(1)求出从6人中随机选出2人,选出的2人中至少有1个女运动员的基本事件数,计算对应的概率值;(2)根据题目中的数据,画出茎叶图,计算甲、乙运动员的平均成绩与方差,比较大小即可得出结论.
【考点精析】利用茎叶图和极差、方差与标准差对题目进行判断即可得到答案,需要熟知茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少;标准差和方差越大,数据的离散程度越大;标准差和方程为0时,样本各数据全相等,数据没有离散性;方差与原始数据单位不同,解决实际问题时,多采用标准差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
 )的部分图象如图所示.
)的部分图象如图所示.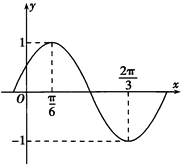
(1)求函数f(x)的解析式,并写出f(x)的单调减区间;
(2)已知△ABC的内角分别是A,B,C,A为锐角,且f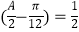 ,求cosA的值.
,求cosA的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
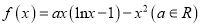 恰有两个极值点
恰有两个极值点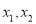 ,且
,且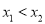 .
.(1)求实数
 的取值范围;
的取值范围;(2)若不等式
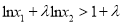 恒成立,求实数
恒成立,求实数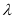 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于x的一元二次方程x2﹣2ax+b2=0.
(1)若a是从0、1、2、3四个数中任取的一个数,b是从0、1、2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]内任取的一个数,b是从区间[0,2]内任取的一个数,求上述方程有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
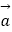 =(
=( 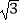 sinx,m+cosx),
sinx,m+cosx),  =(cosx,﹣m+cosx),且f(x)=
=(cosx,﹣m+cosx),且f(x)= 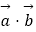
(1)求函数f(x)的解析式;
(2)当x∈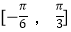 时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2cosxsin(x﹣
 )+
)+  .
.
(1)求函数f(x)的对称轴方程;
(2)若方程sin2x+2|f(x+ )|﹣m+1=0在x∈
)|﹣m+1=0在x∈  上有三个实数解,求实数m的取值范围.
上有三个实数解,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
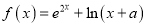 .
.(1)当
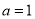 时,求
时,求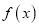 在
在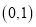 处的切线方程;
处的切线方程;(2)若存在
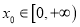 ,使得
,使得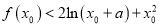 成立,求实数
成立,求实数 的取值范围.
的取值范围.
相关试题

