【题目】如图所示,平面多边形![]() 中,AE=ED,AB=BD,且
中,AE=ED,AB=BD,且![]() ,现沿直线
,现沿直线![]() ,将
,将![]() 折起,得到四棱锥
折起,得到四棱锥![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,求PD与平面
,求PD与平面![]() 所成角的正弦值.
所成角的正弦值.
参考答案:
【答案】(1)见解析;(2)正弦值为![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连
,连![]() ,由题意可得
,由题意可得![]() 且
且![]() ,则有
,则有![]() 平面
平面![]() ,可得结论;(2)法一:以O为坐标原点,OB, OD, OP所在的直线为x,y,z轴建立空间直角坐标系,求出平面PAB的一个法向量,再利用向量的夹角公式求解即可;法二:利用等积法:由
,可得结论;(2)法一:以O为坐标原点,OB, OD, OP所在的直线为x,y,z轴建立空间直角坐标系,求出平面PAB的一个法向量,再利用向量的夹角公式求解即可;法二:利用等积法:由![]() 得
得![]() =
= ![]() ,求出点D到平面PAB的距离为h
,求出点D到平面PAB的距离为h![]() ,设PD与平面
,设PD与平面![]() 所成角为
所成角为![]() ,则
,则![]() =
=![]() =
=![]() =
=![]() .
.
解析:
(1)证明:取![]() 的中点
的中点![]() ,连
,连![]() ,
,

∵![]() ,即
,即![]() ,
,
∴![]() 且
且![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,
,
∴![]() .
.
(2)∵OP=1,OB=2,
![]() ,
,
∴![]() ,
,
∴OP、OB、OD两两互相垂直,
以O为坐标原点,OB, OD, OP所在的直线为x,y,z轴建立如图所示空间直角坐标系,
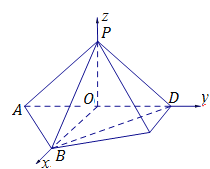
则![]() ,
,
![]() ,
,
设![]() 为平面PAB的一个法向量,则
为平面PAB的一个法向量,则
由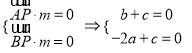 ,
,
令![]() 则得
则得![]() ,
,
∴![]() ,
,
设PD与平面![]() 所成角为
所成角为![]() ,
,
则![]() =
=![]() =
=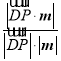 =
=![]() =
=![]() ,
,
故![]() ,
,
即PD与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是
是 在点
在点 处的切线.
处的切线.(
 )求
)求 的解析式.
的解析式.(
 )求证:
)求证:  .
.(
 )设
)设 ,其中
,其中 .若
.若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】求下列函数的最值
(1)求函数
 的最小值.
的最小值.(2)求函数
 的最小值.
的最小值.(3)设
 ,
, ,若
,若 ,求
,求 的最小值.
的最小值.(4)若正数
 ,
, 满足
满足 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于数集
 ,其中
,其中 ,
,  ,定义向量集
,定义向量集 .若对于任意
.若对于任意 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .例如
.例如 具有性质
具有性质 .
.(
 )若
)若 ,且
,且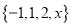 具有性质
具有性质 ,求
,求 的值.
的值.(
 )若
)若 具有性质
具有性质 ,求证:
,求证:  ,且当
,且当 时,
时,  .
.(
 )若
)若 具有性质
具有性质 ,且
,且 ,
,  (
( 为常数),求有穷数列
为常数),求有穷数列 ,
,  ,
,  ,
,  的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),得到如图5的茎叶图,整数位为茎,小数位为叶,如27.1mm的茎为27,叶为1.

(1)试比较甲、乙两种棉花的纤维长度的平均值的大小及方差的大小;(只需写出估计的结论,不需说明理由)
(2)将棉花按纤维长度的长短分成七个等级,分级标准如表:

试分别估计甲、乙两种棉花纤维长度等级为二级的概率;
(3)为进一步检验甲种棉花的其它质量指标,现从甲种棉花中随机抽取4根,记
 为抽取的棉花纤维长度为二级的根数,求
为抽取的棉花纤维长度为二级的根数,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合P={x|a+1≤x≤2a+1},Q={x|x2-3x≤10}.
(1)若a=3,求(RP)∩Q;
(2)若P∪Q=Q,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 是双曲线C:
是双曲线C: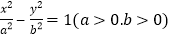 的左,右焦点,O是坐标原点
的左,右焦点,O是坐标原点 过
过 作C的一条渐近线的垂线,垂足为P,若
作C的一条渐近线的垂线,垂足为P,若 ,则C的离心率为
,则C的离心率为

A.
 B. 2 C.
B. 2 C.  D.
D. 
相关试题

