搜索
【题目】在平面直角坐标系
中，已知椭圆
的焦距为
，离心率为
，椭圆的右顶点为
.
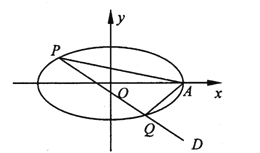
（1）求该椭圆的方程；
（2）过点
作直线
交椭圆于两个不同点
，求证：直线
的斜率之和为定值.
参考答案：
【答案】（1）
（2）直线AP，AQ的斜率之和为定值1.
【解析】试题（1）由题意可知
，
，离心率
，求得
，则
，即可求得椭圆的方程；（2）则直线
的方程：
，代入椭圆方程，由韦达定理及直线的斜率公式，分别求得直线
，
的斜率，即可证明直线，的率之和为定值.
试题解析：（1）由题
所以，
.
所以椭圆C的方程为
（2）当直线PQ的斜率不存在时，不合题意；
当直线PQ的斜率存在时，设直线PQ的方程为，
代入
得
，
设
，
，则：
，
，
，
所以
，
，
又
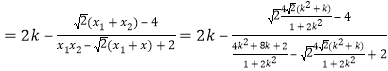=1.
所以直线AP，AQ的斜率之和为定值1.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数y=f（x）的定义在实数集R上的奇函数，且当x∈（﹣∞，0）时，xf′（x）＜f（﹣x）（其中f′（x）是f（x）的导函数），若a=
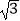f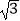（ ），b=（lg3）f（lg3），c=（log2 
）f（log2 ），则（ ）
A.c＞a＞b
B.c＞b＞a
C.a＞b＞c
D.a＞c＞b -
科目： 来源： 题型：
查看答案和解析>>【题目】设点P是曲线y=x3﹣
x+ 
上的任意一点，点P处的切线倾斜角为α，则α的取值范围为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知椭圆
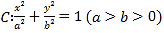的离心率是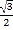
，一个顶点是
．
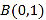（Ⅰ）求椭圆
的方程；（Ⅱ）设
，
是椭圆上异于点
的任意两点，且
．试问：直线
是否恒过一定点？若是，求出该定点的坐标；若不是，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=2cos2x+sin2x﹣4cosx．
（1）求
的值；
（2）求f（x）的最大值和最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】设p：不等式x2+（m﹣1）x+1＞0的解集为R；q：x∈（0，+∞），m≤x+
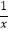恒成立．若“p且q”为假命题，“p或q”为真命题，求实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=x3+bx2+cx﹣1当x=﹣2时有极值，且在x=﹣1处的切线的斜率为﹣3．
（1）求函数f（x）的解析式；
（2）求函数f（x）在区间[﹣1，2]上的最大值与最小值．
相关试题
