【题目】已知函数y=f(x)的定义在实数集R上的奇函数,且当x∈(﹣∞,0)时,xf′(x)<f(﹣x)(其中f′(x)是f(x)的导函数),若a= ![]() f(
f( ![]() ),b=(lg3)f(lg3),c=(log2
),b=(lg3)f(lg3),c=(log2 ![]() )f(log2
)f(log2 ![]() ),则( )
),则( )
A.c>a>b
B.c>b>a
C.a>b>c
D.a>c>b
参考答案:
【答案】A
【解析】解:设F(x)=xf(x),得F'(x)=x'f(x)+xf'(x)=xf'(x)+f(x),
∵当x∈(﹣∞,0)时,xf′(x)<f(﹣x),且f(﹣x)=﹣f(x)
∴当x∈(﹣∞,0)时,xf′(x)+f(x)<0,即F'(x)<0
由此可得F(x)=xf(x)在区间(﹣∞,0)上是减函数,
∵函数y=f(x)是定义在实数集R上的奇函数,
∴F(x)=xf(x)是定义在实数集R上的偶函数,在区间(0,+∞)上F(x)=xf(x)是增函数.
∵0<lg3<lg10=1, ![]() ∈(1,2)
∈(1,2)
∴F(2)>F( ![]() )>F(lg3)
)>F(lg3)
∵ ![]() =﹣2,从而F(
=﹣2,从而F( ![]() )=F(﹣2)=F(2)
)=F(﹣2)=F(2)
∴F( ![]() )>F(
)>F( ![]() )>F(lg3)
)>F(lg3)
即 ![]() >
> ![]() >(lg3)f(lg3),得c>a>b
>(lg3)f(lg3),得c>a>b
所以答案是:A
【考点精析】本题主要考查了对数值大小的比较和导数的几何意义的相关知识点,需要掌握几个重要的对数恒等式:![]() ,
,![]() ,
,![]() ;常用对数:
;常用对数:![]() ,即
,即![]() ;自然对数:
;自然对数:![]() ,即
,即![]() (其中
(其中![]() …);通过图像,我们可以看出当点
…);通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的参数方程为
 (θ为参数),曲线 C2的极坐标方程为ρcosθ﹣
(θ为参数),曲线 C2的极坐标方程为ρcosθ﹣  ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲线C1的普通方程和曲线 C2的直角坐标方程;
(2)设P为曲线C1上一点,Q为曲线 C2上一点,求|PQ|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣1,1].
(1)求m的值;
(2)若a,b,c∈R,且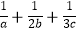 =m,求证:a+2b+3c≥9.
=m,求证:a+2b+3c≥9. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.命题“x∈R,ex>0”的否定是“x∈R,ex>0”
B.命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题
C.“x2+2x≥ax在x∈[1,2]上恒成立”“(x2+2x)min≥(ax)max在x∈[1,2]上恒成立”
D.命题“若a=﹣1,则函数f(x)=ax2+2x﹣1只有一个零点”的逆命题为真命题 -
科目: 来源: 题型:
查看答案和解析>>【题目】设点P是曲线y=x3﹣
 x+
x+  上的任意一点,点P处的切线倾斜角为α,则α的取值范围为 .
上的任意一点,点P处的切线倾斜角为α,则α的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
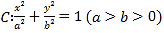 的离心率是
的离心率是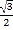 ,一个顶点是
,一个顶点是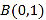 .
.
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设
 ,
, 是椭圆
是椭圆 上异于点
上异于点 的任意两点,且
的任意两点,且 .试问:直线
.试问:直线 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由. -
科目: 来源: 题型:
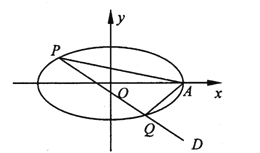
查看答案和解析>>【题目】在平面直角坐标系
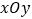 中,已知椭圆
中,已知椭圆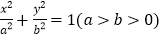 的焦距为
的焦距为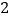 ,离心率为
,离心率为 ,椭圆的右顶点为
,椭圆的右顶点为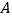 .
.
(1)求该椭圆的方程;
(2)过点
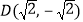 作直线
作直线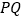 交椭圆于两个不同点
交椭圆于两个不同点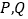 ,求证:直线
,求证:直线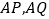 的斜率之和为定值.
的斜率之和为定值.
相关试题

