【题目】已知函数![]() ,
,![]()
(1)求函数![]() 的单调递减区间;
的单调递减区间;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不等的根,求实数
上有两个不等的根,求实数![]() 的取值范围;
的取值范围;
(3)若存在![]() ,当
,当![]() 时,恒有
时,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)由题已知函数![]() ,求函数的单调区间,可按照先求导,再令
,求函数的单调区间,可按照先求导,再令![]() ,又解出对应的不等式的解集,可得;(注意定义域优先)
,又解出对应的不等式的解集,可得;(注意定义域优先)
(2)由![]() 在区间上有两个根,可通过构造函数
在区间上有两个根,可通过构造函数![]() ,转而利用导数考察函数的单调性和极值,再结合零点判定定理可建立关于
,转而利用导数考察函数的单调性和极值,再结合零点判定定理可建立关于![]() 不等式组,可求。
不等式组,可求。
(3)由![]() ,都有
,都有![]() 为恒成立问题,可构造函数
为恒成立问题,可构造函数![]() ,又
,又![]() ,只需函数
,只需函数![]() 在给定的区间上单调递增即可,可利用导数,让导函数再区间上恒大于零可解出
在给定的区间上单调递增即可,可利用导数,让导函数再区间上恒大于零可解出![]() 的取值范围.
的取值范围.
试题解析:解:(1)因为函数![]() 的定义域为
的定义域为![]() ,
,
且![]() ,
,
令![]() ,即
,即![]() 解之得
解之得![]() :
:
所以函数![]() 的单调递减区间为
的单调递减区间为![]()
(2)令![]() ,
,
且定义域为![]()
所以![]() ,令
,令![]() ,
,![]() ,
,
列表如下:
|
| 1 |
|
| + | 0 | - |
| 递增 | 极大值 | 递减 |
所以函数![]() 在区间
在区间![]() 先单调递减后单调递增,故要使
先单调递减后单调递增,故要使![]() 有两个不等的根,
有两个不等的根,
只须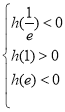 即
即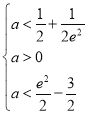 所以
所以![]()
(3)令![]() ,且
,且![]()
要使存在![]() ,当
,当![]() 时,恒有
时,恒有![]() ,
,
则只须![]() 即可,
即可,
也就是存在![]() ,当
,当![]() 时函数
时函数![]() 是单调递增的,
是单调递增的,
又因为![]() ,只须在
,只须在![]() 时
时![]() 成立,
成立,
即![]() ,解得
,解得![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=(1,2),b=(-2,n),a与b的夹角是45°.
(1) 求b;
(2) 若c与b同向,且a与c-a垂直,求向量c的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=
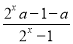 为奇函数.
为奇函数.(1) 求a的值;
(2) 判断f(x)的单调性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,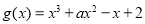 ,
,(1)若函数
 的两个极值点为
的两个极值点为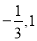 ,求函数
,求函数 的解析式;
的解析式;(2)在(1)的条件下,求函数
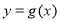 的图象过点
的图象过点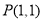 的切线方程;
的切线方程;(3)对一切
 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在
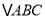 中,角
中,角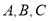 的对边分别为
的对边分别为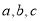 ,若
,若 (
(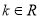 ).
).(1)判断
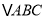 的形状;
的形状;(2)若
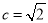 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
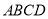 与
与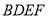 均为菱形,
均为菱形,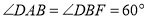 ,且
,且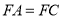 .
.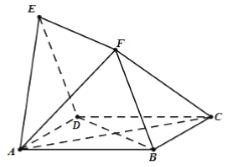
(1)求证:
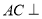 平面
平面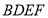 ;
;(2)求证:
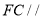 平面
平面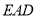 ;
;(3)求二面角
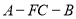 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
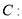

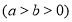 的离心率为
的离心率为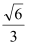 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为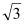 .
.(1) 求椭圆
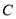 的方程;
的方程;(2) 设直线
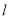 与椭圆
与椭圆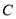 交于
交于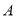 、
、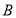 两点,坐标原点
两点,坐标原点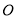 到直线
到直线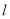 的距离为
的距离为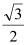 ,求
,求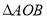 面积的最大值.
面积的最大值.
相关试题

