【题目】已知函数![]() ,
,![]() ,
,
(1)若函数![]() 的两个极值点为
的两个极值点为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象过点
的图象过点![]() 的切线方程;
的切线方程;
(3)对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
参考答案:
【答案】(1)![]() (2)x+y-2=0 (3) a≥-2
(2)x+y-2=0 (3) a≥-2
【解析】函数![]() 的两个极值点处导数为0 ,g’(x)=3x2+2ax-1带入
的两个极值点处导数为0 ,g’(x)=3x2+2ax-1带入![]() 即可;
即可;
要求函数![]() 的图象过点
的图象过点![]() 的切线方程,先求函数在点
的切线方程,先求函数在点![]() 处的导数即斜率,在用点斜式求出方程;恒成立求实数
处的导数即斜率,在用点斜式求出方程;恒成立求实数![]() 的取值范围时,一般分离参数,2a≥2lnx-3x-
的取值范围时,一般分离参数,2a≥2lnx-3x-![]() 再在最值处成立即可。
再在最值处成立即可。
解:(1)g’(x)=3x2+2ax-1由题意:![]()
![]()
(2)由(1)可得:g(x)=x3-x2-x+2(1o)若P为切点,则切线方程为:y=1
2 o若P不是切点,设切点Q(x0,y0)∴切线方程为y-y0=(3x02-2x0-1)(x-x0)
1-(x03-x02-x0+2)=(3x02-2x0-1)(1-x0) 2x0(x0-1)2=0 ∴x0=0 ∴切点(0,2)
∴切线方程:x+y-2=0
(3)2xlnx≤3x2+2ax-1+2 ∴2ax≥2xlnx-3x2-1 ∵x>0 ∴2a≥2lnx-3x-![]()
令ln(x)=2lnx-3x-![]()
![]()
x(0,1)1(1,+∞)
h’(x)+0-
h(x)↑极大值↓
∴h(x) ≤h(1)=-4 ∴2a≥-4 a≥-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某投资公司拟投资开发某项新产品,市场评估能获得10~1 000万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不低于1万元,同时不超过投资收益的20%.
(1) 设奖励方案的函数模型为f(x),试用数学语言表述公司对奖励方案的函数模型f(x)的基本要求;
(2) 公司能不能用函数f(x)=
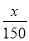 +2作为预设的奖励方案的模型函数?
+2作为预设的奖励方案的模型函数? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=(1,2),b=(-2,n),a与b的夹角是45°.
(1) 求b;
(2) 若c与b同向,且a与c-a垂直,求向量c的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=
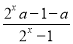 为奇函数.
为奇函数.(1) 求a的值;
(2) 判断f(x)的单调性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
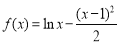 ,
,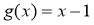
(1)求函数
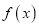 的单调递减区间;
的单调递减区间;(2)若关于
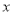 的方程
的方程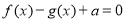 在区间
在区间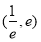 上有两个不等的根,求实数
上有两个不等的根,求实数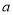 的取值范围;
的取值范围;(3)若存在
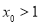 ,当
,当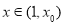 时,恒有
时,恒有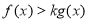 ,求实数
,求实数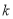 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
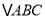 中,角
中,角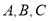 的对边分别为
的对边分别为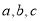 ,若
,若 (
(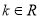 ).
).(1)判断
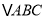 的形状;
的形状;(2)若
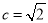 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
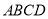 与
与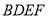 均为菱形,
均为菱形,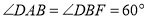 ,且
,且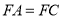 .
.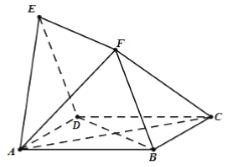
(1)求证:
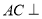 平面
平面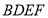 ;
;(2)求证:
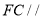 平面
平面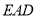 ;
;(3)求二面角
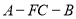 的余弦值.
的余弦值.
相关试题

