【题目】已知a=(1,2),b=(-2,n),a与b的夹角是45°.
(1) 求b;
(2) 若c与b同向,且a与c-a垂直,求向量c的坐标.
参考答案:
【答案】(1)(-2,6).(2)(-1,3)
【解析】试题分析(1)由向量夹角公式、向量模的坐标表示、向量数量积的坐标表示得关于n的方程,解方程可得n=6,即得b;(2)由向量平行可设c=λb(λ>0),由向量垂直可得数量积为零,根据向量数量积坐标表示可得关于λ的方程,解得λ值 ,即得向量c的坐标
试题解析:解:(1) ∵ a·b=2n-2,|a|=![]() ,|b|=
,|b|=![]() ,
,
∴ cos 45°=![]() =
=![]() ,
,
∴ 3n2-16n-12=0(n>1),
∴ n=6或n=-![]() (舍去),∴ b=(-2,6).
(舍去),∴ b=(-2,6).
(2) 由(1)知,a·b=10,|a|2=5.
∵ c与b同向,故可设c=λb(λ>0).
∵ a与c-a垂直,∴ (c-a)·a=0,
∴ λb·a-|a|2=0,∴ λ=![]() =
=![]() =
=![]() .
.
∴ c=![]() b=(-1,3).
b=(-1,3).
-
科目: 来源: 题型:
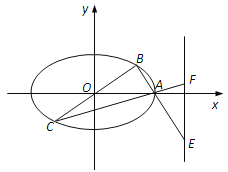
查看答案和解析>>【题目】在平面直角坐标系
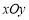 中,椭圆
中,椭圆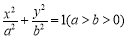 的离心率为
的离心率为 ,右顶点为
,右顶点为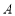 ,直线
,直线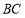 过原点
过原点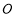 ,且点
,且点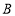 在x轴的上方,直线
在x轴的上方,直线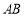 与
与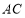 分别交直线
分别交直线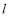 :
: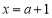 于点
于点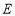 、
、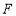 .
.
(1)若点
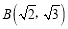 ,求椭圆的方程及△ABC的面积;
,求椭圆的方程及△ABC的面积;(2)若
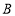 为动点,设直线
为动点,设直线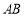 与
与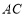 的斜率分别为
的斜率分别为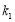 、
、 .
.①试问
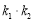 是否为定值?若为定值,请求出;否则,请说明理由;
是否为定值?若为定值,请求出;否则,请说明理由;②求△AEF的面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
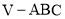 中,平面
中,平面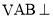 平面
平面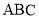 ,
,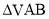 为等边三角形,
为等边三角形,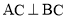 且
且 ,
,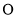 ,
,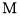 分别为
分别为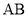 ,
,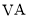 的中点.
的中点.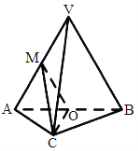
(I)求证:
 平面
平面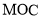 ;
;(II)求证:平面
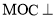 平面
平面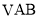 ;
;(III)求三棱锥
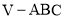 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
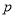 :
: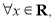
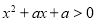 ;
; 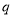 :关于
:关于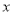 的方程
的方程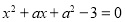 的两根之差的绝对值大于3.如果
的两根之差的绝对值大于3.如果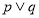 为真命题,
为真命题,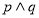 为假命题,求实数
为假命题,求实数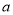 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
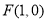 ,直线
,直线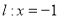 ,动点
,动点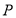 到点
到点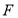 的距离等于它到直线
的距离等于它到直线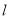 的距离.
的距离.(Ⅰ)求点
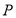 的轨迹
的轨迹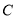 的方程;
的方程;(Ⅱ)是否存在过
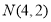 的直线
的直线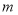 ,使得直线
,使得直线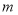 被曲线
被曲线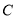 截得的弦
截得的弦 恰好被点
恰好被点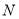 所平分?
所平分? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 椭圆
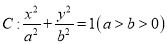 的离心率是
的离心率是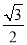 ,点
,点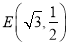 在椭圆上, 设点
在椭圆上, 设点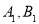 分别是椭圆的右顶点和上顶点, 过 点
分别是椭圆的右顶点和上顶点, 过 点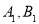 引椭圆
引椭圆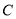 的两条弦
的两条弦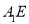 、
、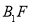 .
.(1)求椭圆
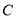 的方程;
的方程;(2)若直线
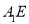 与
与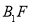 的斜率是互为相反数.
的斜率是互为相反数.①直线
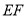 的斜率是否为定值?若是求出该定值, 若不是,说明理由;
的斜率是否为定值?若是求出该定值, 若不是,说明理由;②设
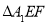 、
、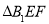 的面积分别为
的面积分别为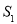 和
和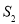 ,求
,求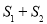 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a|=4,|b|=8,a与b的夹角是120°.
(1) 计算:① |a+b|,② |4a-2b|;
(2) 当k为何值时,(a+2b)⊥(ka-b)?
相关试题

