【题目】已知函数![]()
(1)求函数的定义域;
(2)判定函数![]() 在
在![]() 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(3)若当![]() 时,
时, ![]() 恒成立,求正整数
恒成立,求正整数![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() (2)减函数 (3)3
(2)减函数 (3)3
【解析】试题分析:
(1)结合函数的解析式可得函数的定义域为![]() ;
;
(2)对函数 求导,结合题意和导函数的解析式可得![]() =-
=-![]()
![]() <0,所以函数f(x)在区间(-1,0)上是减函数.
<0,所以函数f(x)在区间(-1,0)上是减函数.
(3)首先由不等式的性质可得k的最大值不大于3,然后结合导函数的性质可得![]() 满足题意,即正整数
满足题意,即正整数![]() 的最大值是3.
的最大值是3.
试题解析:
解:(Ⅰ)函数的定义域为![]()
(Ⅱ)![]() =
=![]()
![]() =-
=-![]()
![]() 设
设![]() ,
,
故g(x)在(-1,0)上是减函数,而g(x)>g(0)=1>0,
故![]() =-
=-![]()
![]() <0,
<0,
所以函数f(x)在区间(-1,0)上是减函数.
(III)当x>0时,f(x)>![]() 恒成立, 令x=1有k<2
恒成立, 令x=1有k<2![]()
又k为正整数.∴k的最大值不大于3.
下面证明当k=3时,f(x)>![]() (x>0)恒成立.
(x>0)恒成立.
即证当x>0时, ![]()
![]() +1-2x>0恒成立.
+1-2x>0恒成立.
令g(x)=![]()
![]() +1-2x,则
+1-2x,则![]() =
=![]() -1,
-1,
当x>e-1时, ![]() >0;当0<x<e-1时,
>0;当0<x<e-1时, ![]() <0.
<0.
∴当x=e-1时,g(x)取得最小值g(e-1)=3-e>0.
∴当x>0时, ![]()
![]() +1-2x>0恒成立.
+1-2x>0恒成立.
因此正整数k的最大值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,曲线
,曲线 在点
在点 处的切线与
处的切线与 轴交点的横坐标为
轴交点的横坐标为 .
.(1)求
 ;
;(2)证明:当
 时,曲线
时,曲线 与直线
与直线 只有一个交点.
只有一个交点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
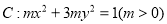 的长轴长为
的长轴长为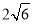 ,
,  为坐标原点.
为坐标原点.(1)求椭圆
 的方程和离心率.
的方程和离心率.(2)设点
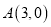 ,动点
,动点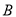 在
在 轴上,动点
轴上,动点 在椭圆
在椭圆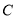 上,且点
上,且点 在
在 轴的右侧.若
轴的右侧.若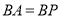 ,求四边形
,求四边形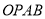 面积的最小值.
面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若存在两个正实数
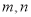 ,使得等式
,使得等式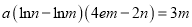 成立(其中
成立(其中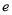 为自然对数的底数),则实数
为自然对数的底数),则实数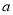 的取值范围是( )
的取值范围是( )A.
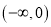 B.
B. 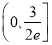 C.
C. 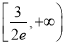 D.
D. 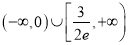
-
科目: 来源: 题型:
查看答案和解析>>【题目】从集合
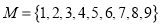 中,抽取三个不同的元素构成子集
中,抽取三个不同的元素构成子集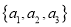 .
.(1)求对任意的
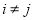 满足
满足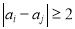 的概率;
的概率;(2)若
 成等差数列,设其公差为
成等差数列,设其公差为 ,求随机变量
,求随机变量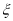 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】若数列
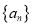 和
和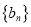 的项数均为
的项数均为 ,则将数列
,则将数列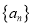 和
和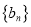 的距离定义为
的距离定义为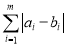 .
.(1)求数列1,3,5,6和数列2,3,10,7的距离.
(2)记
 为满足递推关系
为满足递推关系 的所有数列
的所有数列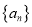 的集合,数列
的集合,数列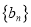 和
和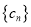 为
为 中的两个元素,且项数均为
中的两个元素,且项数均为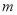 .若
.若 ,
,  ,数列
,数列 和
和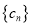 的距离小于2016,求
的距离小于2016,求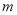 的最大值.
的最大值.(3)记
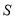 是所有7项数列
是所有7项数列 (其中
(其中 ,
, 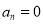 或
或 )的集合,
)的集合, 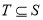 ,且
,且 中的任何两个元素的距离大于或等于3.求证:
中的任何两个元素的距离大于或等于3.求证: 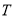 中的元素个数小于或等于16.
中的元素个数小于或等于16. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列4个命题:
①“若
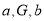 成等比数列,则
成等比数列,则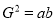 ”的逆命题;
”的逆命题;②“如果
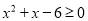 ,则
,则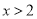 ”的否命题;
”的否命题;③在
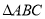 中,“若
中,“若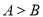 ”则“
”则“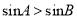 ”的逆否命题;
”的逆否命题;④当
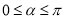 时,若
时,若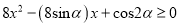 对
对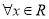 恒成立,则
恒成立,则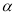 的取值范围是
的取值范围是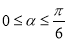 .
.其中真命题的序号是__________.
相关试题

