【题目】下列4个命题:
①“若![]() 成等比数列,则
成等比数列,则![]() ”的逆命题;
”的逆命题;
②“如果![]() ,则
,则![]() ”的否命题;
”的否命题;
③在![]() 中,“若
中,“若![]() ”则“
”则“![]() ”的逆否命题;
”的逆否命题;
④当![]() 时,若
时,若![]() 对
对![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是![]() .
.
其中真命题的序号是__________.
参考答案:
【答案】②,③
【解析】①“若a、G、b成等比数列,则G2=ab”的逆命题为“若G2=ab,则a、G、b成等比数列”,
不正确,比如a=G=b=0,则a、G、b不成等比数列,故①错;
②“如果x2+x60,则x>2”的否命题为“②“如果x2+x6<0,则x2”的否命题”,
由x2+x6<0,可得3<x<2,推得x2,故②对;
③在△ABC中,“若A>B”“a>b”“2RsinA>2RsinB”“sinA>sinB”(R为外接圆的半径)则其逆否命题正确,故③对;
④当0απ时,若8x2(8sinα)x+cos2α0对x∈R恒成立,即有△=64sin2α32cos2α0,
即有12cos2α0,即为cos2α![]() ,可得
,可得![]() ,
,
解得![]() ,故④错。
,故④错。
故真命题的序号是②③。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
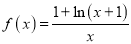
(1)求函数的定义域;
(2)判定函数
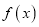 在
在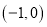 的单调性,并证明你的结论;
的单调性,并证明你的结论;(3)若当
 时,
时, 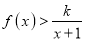 恒成立,求正整数
恒成立,求正整数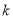 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从集合
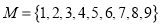 中,抽取三个不同的元素构成子集
中,抽取三个不同的元素构成子集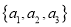 .
.(1)求对任意的
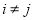 满足
满足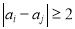 的概率;
的概率;(2)若
 成等差数列,设其公差为
成等差数列,设其公差为 ,求随机变量
,求随机变量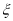 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】若数列
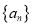 和
和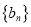 的项数均为
的项数均为 ,则将数列
,则将数列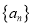 和
和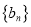 的距离定义为
的距离定义为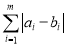 .
.(1)求数列1,3,5,6和数列2,3,10,7的距离.
(2)记
 为满足递推关系
为满足递推关系 的所有数列
的所有数列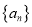 的集合,数列
的集合,数列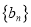 和
和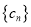 为
为 中的两个元素,且项数均为
中的两个元素,且项数均为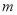 .若
.若 ,
,  ,数列
,数列 和
和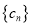 的距离小于2016,求
的距离小于2016,求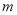 的最大值.
的最大值.(3)记
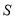 是所有7项数列
是所有7项数列 (其中
(其中 ,
, 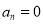 或
或 )的集合,
)的集合, 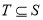 ,且
,且 中的任何两个元素的距离大于或等于3.求证:
中的任何两个元素的距离大于或等于3.求证: 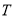 中的元素个数小于或等于16.
中的元素个数小于或等于16. -
科目: 来源: 题型:
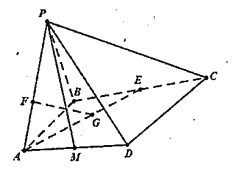
查看答案和解析>>【题目】如图,在四棱锥
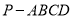 中,侧面
中,侧面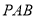 与底面
与底面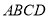 垂直,
垂直, 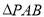 为正三角形,
为正三角形, 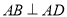 ,
, 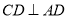 ,点
,点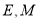 分别为线段
分别为线段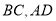 的中点,
的中点, 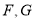 分别为线段
分别为线段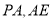 上一点,且
上一点,且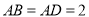 ,
, 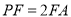 .
.
(1)当
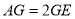 时,求证:
时,求证: 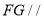 平面
平面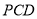 ;
;(2)试问:直线
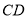 上是否存在一点
上是否存在一点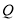 ,使得平面
,使得平面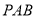 与平面
与平面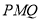 所成锐二面角的大小为
所成锐二面角的大小为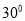 ,若存在,求
,若存在,求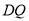 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
分公司名称
雅雨
雅鱼
雅女
雅竹
雅茶
月销售额
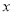 (万元)
(万元)3
5
6
7
9
月利润额
 (万元)
(万元)2
3
3
4
5
在统计中发现月销售额
 和月利润额
和月利润额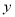 具有线性相关关系.
具有线性相关关系.(1)根据如下的参考公式与参考数据,求月利润额
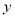 与月销售额
与月销售额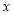 之间的线性回归方程;
之间的线性回归方程;(2)若该总公司还有一个分公司“雅果”月销售额为10万元,试估计它的月利润额是多少?
(参考公式:
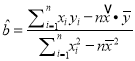 ,
, 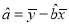 ,其中:
,其中: 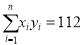 ,
, 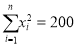 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
A.[选修4-1:几何证明选讲]
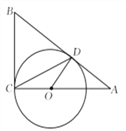
如图,
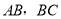 分别与圆
分别与圆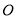 相切于点
相切于点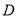 ,
, 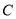 ,
, 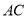 经过圆心
经过圆心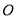 ,且
,且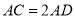 ,求证:
,求证: 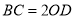 .
.
B.[选修4-2:矩阵与变换]
在平面直角坐标系中,已知点
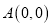 ,
, 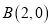 ,
, 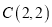 ,
, 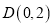 ,先将正方形
,先将正方形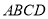 绕原点
绕原点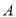 逆时针旋转
逆时针旋转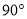 ,再将所得图形的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵
,再将所得图形的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵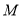 .
.C.[选修4-4:坐标系与参数方程]
在平面直角坐标系
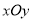 中,已知曲线
中,已知曲线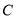 的参数方程为
的参数方程为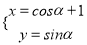 (
(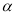 为参数).现以
为参数).现以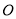 为极点,
为极点, 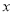 轴的正半轴为极轴,建立极坐标系,求曲线
轴的正半轴为极轴,建立极坐标系,求曲线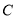 的极坐标方程.
的极坐标方程.D.[选修4-5:不等式选讲]
已知
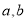 为互不相等的正实数,求证:
为互不相等的正实数,求证: 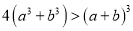 .
.
相关试题

