【题目】若数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将数列
,则将数列![]() 和
和![]() 的距离定义为
的距离定义为![]() .
.
(1)求数列1,3,5,6和数列2,3,10,7的距离.
(2)记![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,数列
的集合,数列![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() .若
.若![]() ,
, ![]() ,数列
,数列![]() 和
和![]() 的距离小于2016,求
的距离小于2016,求![]() 的最大值.
的最大值.
(3)记![]() 是所有7项数列
是所有7项数列![]() (其中
(其中![]() ,
, ![]() 或
或![]() )的集合,
)的集合, ![]() ,且
,且![]() 中的任何两个元素的距离大于或等于3.求证:
中的任何两个元素的距离大于或等于3.求证: ![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
参考答案:
【答案】(1)7;(2)3455;(3)见解析.
【解析】(1)根据题意,将两数列对应代入计算,问题即可得解;(2)由题意,根据递推关系,不难发现数列![]() 是以4为周期的数列,由此可确定数列
是以4为周期的数列,由此可确定数列![]() 亦为周期数列,由其首项即可知对应数列各项,依据定义当项数
亦为周期数列,由其首项即可知对应数列各项,依据定义当项数![]() 越大时,其距离也呈周期性且越大,从而问题可得解;(3)根据题意,这里可以考虑采用反证法来证明,首先假设问题不成立,再通过特殊赋值法,依据定义进行运算,发现与条件相矛盾,从而问题可得证.
越大时,其距离也呈周期性且越大,从而问题可得解;(3)根据题意,这里可以考虑采用反证法来证明,首先假设问题不成立,再通过特殊赋值法,依据定义进行运算,发现与条件相矛盾,从而问题可得证.
试题解析:(1)由题得数列1,3,5,6和数列2,3,10,7的距离为7.
(2)设![]() ,其中
,其中![]() 且
且![]() .
.
由![]() ,
,
得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,….
,….
所以![]() ,
, ![]() ,….
,….
因此集合![]() 中的所有数列都具有周期性,且周期为4.
中的所有数列都具有周期性,且周期为4.
所以数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
,
数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() .
.
因为![]() ,
,
所以项数![]() 越大,数列
越大,数列![]() 和
和![]() 的距离越大.
的距离越大.
因为![]() ,
,
而![]()
![]() ,
,
因此,当![]() 时,
时, ![]() .
.
故![]() 的最大值为3455.
的最大值为3455.
(3)假设![]() 中的元素个数大于或等于17.
中的元素个数大于或等于17.
因为数列![]() 中,
中, ![]() 或1,
或1,
所以仅由数列前三项组成的数组(![]() ,
, ![]() ,
, ![]() )有且只有8个:(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1).
)有且只有8个:(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1).
那么这17个元素之中必有3个具有相同的![]() ,
, ![]() ,
, ![]() .
.
设这3个元素分别为![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() .
.
因为这3个元素中每两个元素的距离大于或等于3,
所以在![]() 与
与![]() 中,
中, ![]()
![]() 至少有3个成立.
至少有3个成立.
不妨设![]() ,
, ![]() ,
, ![]() .
.
由题意得![]() ,
, ![]() 中一个等于0,另一个等于1.
中一个等于0,另一个等于1.
又因为![]() 或1,所以
或1,所以![]() 和
和![]() 中必有一个成立.
中必有一个成立.
同理得: ![]() 和
和![]() 中必有一个成立,
中必有一个成立, ![]() 和
和![]() 中必有一个成立,
中必有一个成立,
所以“![]()
![]() 中至少有两个成立”和“
中至少有两个成立”和“![]()
![]() 中至少有两个成立”中必有一个成立.
中至少有两个成立”中必有一个成立.
故![]() 和
和![]() 中必有一个成立,这与题意矛盾.
中必有一个成立,这与题意矛盾.
所以![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若存在两个正实数
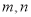 ,使得等式
,使得等式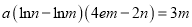 成立(其中
成立(其中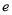 为自然对数的底数),则实数
为自然对数的底数),则实数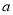 的取值范围是( )
的取值范围是( )A.
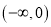 B.
B. 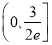 C.
C. 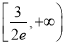 D.
D. 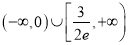
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
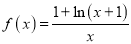
(1)求函数的定义域;
(2)判定函数
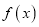 在
在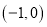 的单调性,并证明你的结论;
的单调性,并证明你的结论;(3)若当
 时,
时, 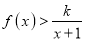 恒成立,求正整数
恒成立,求正整数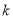 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从集合
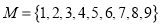 中,抽取三个不同的元素构成子集
中,抽取三个不同的元素构成子集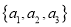 .
.(1)求对任意的
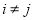 满足
满足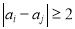 的概率;
的概率;(2)若
 成等差数列,设其公差为
成等差数列,设其公差为 ,求随机变量
,求随机变量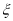 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列4个命题:
①“若
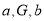 成等比数列,则
成等比数列,则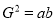 ”的逆命题;
”的逆命题;②“如果
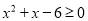 ,则
,则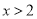 ”的否命题;
”的否命题;③在
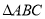 中,“若
中,“若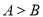 ”则“
”则“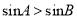 ”的逆否命题;
”的逆否命题;④当
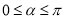 时,若
时,若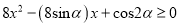 对
对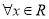 恒成立,则
恒成立,则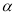 的取值范围是
的取值范围是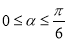 .
.其中真命题的序号是__________.
-
科目: 来源: 题型:
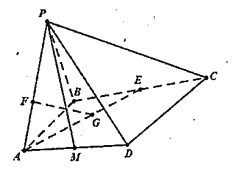
查看答案和解析>>【题目】如图,在四棱锥
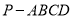 中,侧面
中,侧面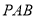 与底面
与底面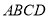 垂直,
垂直, 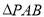 为正三角形,
为正三角形, 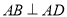 ,
, 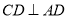 ,点
,点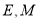 分别为线段
分别为线段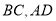 的中点,
的中点, 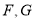 分别为线段
分别为线段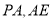 上一点,且
上一点,且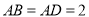 ,
, 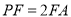 .
.
(1)当
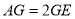 时,求证:
时,求证: 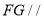 平面
平面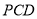 ;
;(2)试问:直线
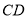 上是否存在一点
上是否存在一点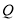 ,使得平面
,使得平面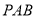 与平面
与平面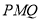 所成锐二面角的大小为
所成锐二面角的大小为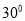 ,若存在,求
,若存在,求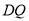 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
分公司名称
雅雨
雅鱼
雅女
雅竹
雅茶
月销售额
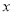 (万元)
(万元)3
5
6
7
9
月利润额
 (万元)
(万元)2
3
3
4
5
在统计中发现月销售额
 和月利润额
和月利润额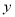 具有线性相关关系.
具有线性相关关系.(1)根据如下的参考公式与参考数据,求月利润额
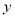 与月销售额
与月销售额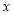 之间的线性回归方程;
之间的线性回归方程;(2)若该总公司还有一个分公司“雅果”月销售额为10万元,试估计它的月利润额是多少?
(参考公式:
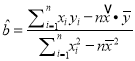 ,
, 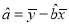 ,其中:
,其中: 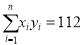 ,
, 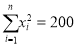 )
)
相关试题

