【题目】若存在两个正实数![]() ,使得等式
,使得等式![]() 成立(其中
成立(其中![]() 为自然对数的底数),则实数
为自然对数的底数),则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】由3m+a(2n4em)(lnnlnm)=0,得![]() ,即
,即![]() ,
,
即设![]() ,则t>0,则条件等价为3+2a(t2e)lnt=0,即
,则t>0,则条件等价为3+2a(t2e)lnt=0,即![]() 有解,
有解,
设g(t)=(t2e)lnt,g′(t)=lnt+12et为增函数,∵g′(e)=lne+12ee=1+12=0,
∴当t>e时,g′(t)>0,当0<t<e时,g′(t)<0,
即当t=e时,函数g(t)取得极小值为:g(e)=(e2e)lne=e,即g(t)g(e)=e,
若![]() 有解,则
有解,则![]() ,即
,即![]() ,
,
则a<0或a32e,
故实数a的取值范围是(∞,0)∪[![]() ,+∞).
,+∞).
本题选择D选项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)设
 .
.①若
 ,曲线
,曲线 在
在 处的切线过点
处的切线过点 ,求
,求 的值;
的值;②若
 ,求
,求 在区间
在区间 上的最大值.
上的最大值.(2)设
 在
在 ,
,  两处取得极值,求证:
两处取得极值,求证:  ,
,  不同时成立.
不同时成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,曲线
,曲线 在点
在点 处的切线与
处的切线与 轴交点的横坐标为
轴交点的横坐标为 .
.(1)求
 ;
;(2)证明:当
 时,曲线
时,曲线 与直线
与直线 只有一个交点.
只有一个交点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
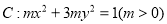 的长轴长为
的长轴长为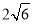 ,
,  为坐标原点.
为坐标原点.(1)求椭圆
 的方程和离心率.
的方程和离心率.(2)设点
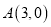 ,动点
,动点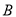 在
在 轴上,动点
轴上,动点 在椭圆
在椭圆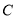 上,且点
上,且点 在
在 轴的右侧.若
轴的右侧.若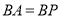 ,求四边形
,求四边形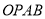 面积的最小值.
面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
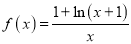
(1)求函数的定义域;
(2)判定函数
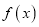 在
在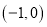 的单调性,并证明你的结论;
的单调性,并证明你的结论;(3)若当
 时,
时, 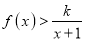 恒成立,求正整数
恒成立,求正整数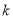 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从集合
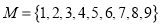 中,抽取三个不同的元素构成子集
中,抽取三个不同的元素构成子集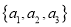 .
.(1)求对任意的
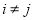 满足
满足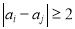 的概率;
的概率;(2)若
 成等差数列,设其公差为
成等差数列,设其公差为 ,求随机变量
,求随机变量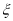 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】若数列
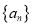 和
和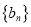 的项数均为
的项数均为 ,则将数列
,则将数列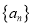 和
和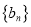 的距离定义为
的距离定义为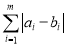 .
.(1)求数列1,3,5,6和数列2,3,10,7的距离.
(2)记
 为满足递推关系
为满足递推关系 的所有数列
的所有数列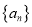 的集合,数列
的集合,数列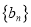 和
和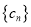 为
为 中的两个元素,且项数均为
中的两个元素,且项数均为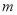 .若
.若 ,
,  ,数列
,数列 和
和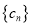 的距离小于2016,求
的距离小于2016,求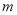 的最大值.
的最大值.(3)记
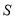 是所有7项数列
是所有7项数列 (其中
(其中 ,
, 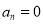 或
或 )的集合,
)的集合, 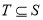 ,且
,且 中的任何两个元素的距离大于或等于3.求证:
中的任何两个元素的距离大于或等于3.求证: 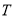 中的元素个数小于或等于16.
中的元素个数小于或等于16.
相关试题

