【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交点的横坐标为
轴交点的横坐标为![]() .
.
(1)求![]() ;
;
(2)证明:当![]() 时,曲线
时,曲线![]() 与直线
与直线![]() 只有一个交点.
只有一个交点.
参考答案:
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(1)![]() ,由导数的几何意义得
,由导数的几何意义得![]() ,故切线方程为
,故切线方程为![]() ,将点
,将点![]() 代入求
代入求![]() ;(2)曲线
;(2)曲线![]() 与直线
与直线![]() 只有一个交点转化为函数
只有一个交点转化为函数![]() 有且只有零点.一般思路往往利用导数求函数的单调区间和极值点,从而判断函数大致图象,再说明与
有且只有零点.一般思路往往利用导数求函数的单调区间和极值点,从而判断函数大致图象,再说明与![]() 轴只有一个交点.本题首先入手点为
轴只有一个交点.本题首先入手点为![]() ,当
,当![]() 时,
时, ![]() ,且
,且![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 有唯一实根.只需说明当
有唯一实根.只需说明当![]() 时无根即可,因为
时无根即可,因为![]() ,故只需说明
,故只需说明![]() ,进而转化为求函数
,进而转化为求函数![]() 的最小值问题处理.
的最小值问题处理.
(1)![]() ,
, ![]() .曲线
.曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .由题设得,
.由题设得, ![]() ,所以
,所以![]() .
.
(2)由(1)得, ![]() .设
.设![]() .由题设得
.由题设得![]() .当
.当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增, ![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 有唯一实根.当
有唯一实根.当![]() 时,令
时,令![]() ,则
,则![]() .
. ![]()
![]() ,
, ![]() 在
在![]() 单调递减;在
单调递减;在![]() 单调递增.所以
单调递增.所以![]() .所以
.所以![]() 在
在![]() 没有实根,综上,
没有实根,综上, ![]() 在
在![]() 上有唯一实根,即曲线
上有唯一实根,即曲线![]() 与直线
与直线![]() 只有一个交点.
只有一个交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各
个城市,得到观看该节目的人数(单位:千人),如茎叶图所示,其中一个数字被污损.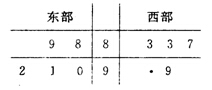
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率;
(2)随着节目的播出,极大激发了观众对成语知识学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了
位观众的周均学习成语知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示),年龄x(岁)
周均学习成语知识时间y(小时)
由表中数据,试求线性回归方程,并预测年龄为
岁观众周均学习成语知识时间.参考公式:
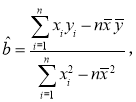 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我海监船在
 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至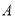 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距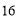 海里的
海里的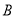 处有一外国船只,且
处有一外国船只,且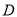 岛位于海监船正东
岛位于海监船正东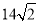 海里处.
海里处.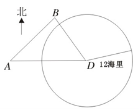
(1)求此时该外国船只与
 岛的距离;
岛的距离;(2)观测中发现,此外国船只正以每小时
 海里的速度沿正南方向航行,为了将该船拦截在离
海里的速度沿正南方向航行,为了将该船拦截在离 岛
岛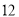 海里处,不让其进入
海里处,不让其进入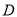 岛
岛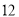 海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据: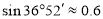 ,
,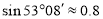 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)设
 .
.①若
 ,曲线
,曲线 在
在 处的切线过点
处的切线过点 ,求
,求 的值;
的值;②若
 ,求
,求 在区间
在区间 上的最大值.
上的最大值.(2)设
 在
在 ,
,  两处取得极值,求证:
两处取得极值,求证:  ,
,  不同时成立.
不同时成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
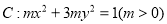 的长轴长为
的长轴长为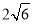 ,
,  为坐标原点.
为坐标原点.(1)求椭圆
 的方程和离心率.
的方程和离心率.(2)设点
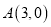 ,动点
,动点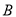 在
在 轴上,动点
轴上,动点 在椭圆
在椭圆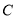 上,且点
上,且点 在
在 轴的右侧.若
轴的右侧.若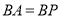 ,求四边形
,求四边形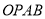 面积的最小值.
面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若存在两个正实数
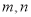 ,使得等式
,使得等式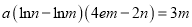 成立(其中
成立(其中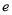 为自然对数的底数),则实数
为自然对数的底数),则实数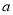 的取值范围是( )
的取值范围是( )A.
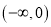 B.
B. 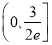 C.
C. 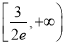 D.
D. 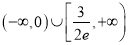
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
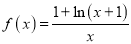
(1)求函数的定义域;
(2)判定函数
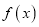 在
在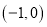 的单调性,并证明你的结论;
的单调性,并证明你的结论;(3)若当
 时,
时, 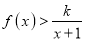 恒成立,求正整数
恒成立,求正整数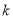 的最大值.
的最大值.
相关试题

