【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】![]() Ⅰ
Ⅰ![]() 详见解析;
详见解析;![]() Ⅱ
Ⅱ![]() ①
①![]() ,②
,②![]() 或
或![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 可以通过已知证明出
可以通过已知证明出![]() 平面PAB,这样就可以证明出
平面PAB,这样就可以证明出![]() ;
;
![]() Ⅱ
Ⅱ![]() 以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,可以求出相应点的坐标,求出平面PBC的法向量为
以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,可以求出相应点的坐标,求出平面PBC的法向量为![]() 、平面PCD的法向量
、平面PCD的法向量![]() ,利用空间向量的数量积,求出二面角
,利用空间向量的数量积,求出二面角![]() 的大小;
的大小;
![]() 求出平面PBC的法向量,利用线面角的公式求出
求出平面PBC的法向量,利用线面角的公式求出![]() 的值.
的值.
证明:![]() Ⅰ
Ⅰ![]() 在图1中,
在图1中,![]() ,
,![]() ,
,

![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() ,
,![]() ,
,
当![]() 沿AD折起时,
沿AD折起时,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,
,![]() 平面PAB,
平面PAB,
又![]() 平面PAB,
平面PAB,![]() .
.
解:![]() Ⅱ
Ⅱ![]() 以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,由于
以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,由于![]() 平面ABCD
平面ABCD
则![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]()
![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
设平面PBC的法向量为![]() y,
y,![]() ,
,
则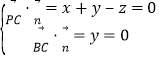 ,取
,取![]() ,得
,得![]() 0,
0,![]() ,
,
设平面PCD的法向量![]() b,
b,![]() ,
,
则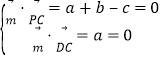 ,取
,取![]() ,得
,得![]() 1,
1,![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,可知为钝角,
,可知为钝角,
则![]() ,
,![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
![]() 设AM与面PBC所成角为
设AM与面PBC所成角为![]() ,
,
![]() 0,
0,![]() ,1,
,1,![]() ,
,![]() ,
,![]() ,
,
平面PBC的法向量![]() 0,
0,![]() ,
,
![]() 直线AM与平面PBC所成的角为
直线AM与平面PBC所成的角为![]() ,
,
![]() ,
,
解得![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设常数a∈R,集合A={x|(x﹣1)(x﹣a)≥0},B={x|x≥a﹣1},若A∪B=R,则a的取值范围为( )
A.(﹣∞,2)
B.(﹣∞,2]
C.(2,+∞)
D.[2,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学为研究函数
 的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设
的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设 ,则
,则 .请你参考这些信息,推知函数
.请你参考这些信息,推知函数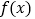 的图象的对称轴是______;函数
的图象的对称轴是______;函数 的零点的个数是______.
的零点的个数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 ,若存在实数,使得
,若存在实数,使得 成立,则x0称为f(x)的“不动点”.
成立,则x0称为f(x)的“不动点”.(1)设函数
 ,求
,求 的不动点;
的不动点;(2)设函数
 ,若对于任意的实数b,函数f(x)恒有两相异的不动点,求实数a的取值范围;
,若对于任意的实数b,函数f(x)恒有两相异的不动点,求实数a的取值范围;(3)设函数
 定义在
定义在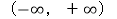 上,证明:若
上,证明:若 存在唯一的不动点,则
存在唯一的不动点,则 也存在唯一的不动点.
也存在唯一的不动点. -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的正六边形ABCDEF中,记以A为起点,其余顶点为终点的向量分别为
 、
、  、
、  、
、  、
、  ;以D为起点,其余顶点为终点的向量分别为
;以D为起点,其余顶点为终点的向量分别为  、
、  、
、  、
、  、
、  .若m、M分别为(
.若m、M分别为(  +
+  +
+  )(
)(  +
+  +
+  )的最小值、最大值,其中{i,j,k}{1,2,3,4,5},{r,s,t}{1,2,3,4,5},则m、M满足( )
)的最小值、最大值,其中{i,j,k}{1,2,3,4,5},{r,s,t}{1,2,3,4,5},则m、M满足( )
A.m=0,M>0
B.m<0,M>0
C.m<0,M=0
D.m<0,M<0
相关试题

