【题目】对于函数![]() ,若存在实数,使得
,若存在实数,使得![]() 成立,则x0称为f(x)的“不动点”.
成立,则x0称为f(x)的“不动点”.
(1)设函数![]() ,求
,求![]() 的不动点;
的不动点;
(2)设函数![]() ,若对于任意的实数b,函数f(x)恒有两相异的不动点,求实数a的取值范围;
,若对于任意的实数b,函数f(x)恒有两相异的不动点,求实数a的取值范围;
(3)设函数![]() 定义在
定义在![]() 上,证明:若
上,证明:若![]() 存在唯一的不动点,则
存在唯一的不动点,则![]() 也存在唯一的不动点.
也存在唯一的不动点.
参考答案:
【答案】(1)![]() 的不动点为-1和2;(2)
的不动点为-1和2;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)设x为不动点,则有![]() ,得
,得![]() ,解方程即可.
,解方程即可.
(2)证法一:设![]() 为
为![]() 不动点,则
不动点,则![]() ,否则设
,否则设![]() ,则
,则![]() 也为
也为![]() 不动点,与已知
不动点,与已知![]() 存在唯一的不动点矛盾.由此能证明若
存在唯一的不动点矛盾.由此能证明若![]() 存在唯一的不动点,则
存在唯一的不动点,则![]() 也存在唯一的不动点.
也存在唯一的不动点.
证法二:设a是![]() 的唯一不动点,
的唯一不动点,![]() .设
.设![]() ,则
,则![]() ,由唯一性,得到
,由唯一性,得到![]() ,从而a是
,从而a是![]() 的不动点.如果f有其它的不动点c,则c也是
的不动点.如果f有其它的不动点c,则c也是![]() 的不动点,由唯一性得
的不动点,由唯一性得![]() ,由此能证明若
,由此能证明若![]() 存在唯一的不动点,则
存在唯一的不动点,则![]() 也存在唯一的不动点.
也存在唯一的不动点.
解:(1)由函数![]() ,得
,得![]()
解得![]() 或
或![]() ,
,
∴![]() 的不动点为-1和2.
的不动点为-1和2.
(2)由![]() 得:
得:![]()
由已知,此方程有相异二实根,![]() 恒成立,即
恒成立,即![]()
即![]() 对任意
对任意![]() 恒成立.
恒成立.![]()
∴实数a的取值范围是![]()
证明:(3)证法一:设函数![]() 定义在
定义在![]() 上,
上,![]() 存在唯一的不动点,
存在唯一的不动点,
首先若![]() 为
为![]() 不动点,则
不动点,则![]()
否则设![]() ,则
,则![]() 也为
也为![]() 不动点,
不动点,
即![]() 不动点不唯一,与已知
不动点不唯一,与已知![]() 存在唯一的不动点矛盾.
存在唯一的不动点矛盾.
∴![]() 有不动点
有不动点![]() 时,
时,![]() 的不动点也是
的不动点也是![]() 的不动点,
的不动点,
∴若![]() 存在唯一的不动点,则
存在唯一的不动点,则![]() 也存在唯一的不动点.
也存在唯一的不动点.
证法二:设a是![]() 的唯一不动点,
的唯一不动点,![]() .
.
设![]() ,则
,则![]()
∴b也是![]() 的不动点.
的不动点.
由唯一性,得到![]() ,∴
,∴![]() ,从而a是
,从而a是![]() 的不动点.
的不动点.
如果f有其它的不动点c,则c也是![]() 的不动点,
的不动点,
由唯一性得![]() ,∴a是
,∴a是![]() 的唯一不动点.
的唯一不动点.
故若![]() 存在唯一的不动点,则
存在唯一的不动点,则![]() 也存在唯一的不动点.
也存在唯一的不动点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知四边形BCDE为直角梯形,
 ,
, ,且
,且 ,A为BE的中点
,A为BE的中点 将
将 沿AD折到
沿AD折到 位置
位置 如图
如图 ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥 .
.
 Ⅰ
Ⅰ 求证
求证 ;
; Ⅱ
Ⅱ 若
若 平面ABCD.
平面ABCD. 求二面角
求二面角 的大小;
的大小; 在棱PC上存在点M,满足
在棱PC上存在点M,满足 ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学为研究函数
 的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设
的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设 ,则
,则 .请你参考这些信息,推知函数
.请你参考这些信息,推知函数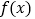 的图象的对称轴是______;函数
的图象的对称轴是______;函数 的零点的个数是______.
的零点的个数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的正六边形ABCDEF中,记以A为起点,其余顶点为终点的向量分别为
 、
、  、
、  、
、  、
、  ;以D为起点,其余顶点为终点的向量分别为
;以D为起点,其余顶点为终点的向量分别为  、
、  、
、  、
、  、
、  .若m、M分别为(
.若m、M分别为(  +
+  +
+  )(
)(  +
+  +
+  )的最小值、最大值,其中{i,j,k}{1,2,3,4,5},{r,s,t}{1,2,3,4,5},则m、M满足( )
)的最小值、最大值,其中{i,j,k}{1,2,3,4,5},{r,s,t}{1,2,3,4,5},则m、M满足( )
A.m=0,M>0
B.m<0,M>0
C.m<0,M=0
D.m<0,M<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线的顶点在坐标原点,焦点F在
 轴正半轴上,过点F的直线交抛物线于A,B两点,线段AB的长是8,AB的中点到
轴正半轴上,过点F的直线交抛物线于A,B两点,线段AB的长是8,AB的中点到 轴的距离是
轴的距离是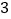 .
.(1)求抛物线的标准方程;
(2)在抛物线上是否存在不与原点重合的点P,使得过点P的直线交抛物线于另一点Q,满足
 ,且直线PQ与抛物线在点P处的切线垂直?并请说明理由.
,且直线PQ与抛物线在点P处的切线垂直?并请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)求
 的定义域;
的定义域;(2)判断
 的奇偶性并给予证明;
的奇偶性并给予证明;(3)求关于x的不等式
 的解集.
的解集.
相关试题

