【题目】(1)求函数![]() 的零点个数;
的零点个数;
(2)证明:当![]() ,函数
,函数![]() 有最小值,设
有最小值,设![]() 的最小值为
的最小值为![]() ,求函数
,求函数![]() 的值域.
的值域.
参考答案:
【答案】(1) 1;(2)![]() .
.
【解析】试题分析:(1)研究函数![]() 的单调性,由零点存在性定理,即可判断函数
的单调性,由零点存在性定理,即可判断函数![]() 的零点个数;(2)
的零点个数;(2)![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 时单调递增,因此,存在唯一
时单调递增,因此,存在唯一![]() ,使得
,使得![]() ,因此
,因此![]() 在
在![]() 处取得最小值
处取得最小值![]() .
.
![]() , 于是
, 于是![]() ,进而求值域即可.
,进而求值域即可.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 内单调递减;
内单调递减;
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 内单调递增;
内单调递增;
故![]() .
.
因为![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() ,
,
所以函数![]() 在区间
在区间![]() 内无零点.
内无零点.
因为![]() ,
,![]() ,
,
又![]() 在区间
在区间![]() 内单调递增,
内单调递增,
根据零点存在性定理,得
函数![]() 在区间
在区间![]() 内有且只有一个零点.
内有且只有一个零点.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 的零点个数为1.
的零点个数为1.
(2)![]() ,
,
则![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 时单调递增,
时单调递增,
对任意![]() ,
,![]() ,
,![]() ,
,
因此,存在唯一![]() ,使得
,使得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
因此![]() 在
在![]() 处取得最小值
处取得最小值![]() .
.
![]() ,
,
![]() ,
,
于是![]() ,
,
由![]() ,
,
得![]() 在
在![]() 单调递减,
单调递减,
所以,由![]() ,得
,得![]() ,
,
![]() ,
,
因为![]() 单调递减,
单调递减,
对任意![]() ,存在唯一的
,存在唯一的![]() ,
,![]() ,使得
,使得![]() ,
,
所以![]() 的值域是
的值域是![]() .
.
综上,当![]() ,函数
,函数![]() 有最小值.
有最小值.
![]() 的值域是
的值域是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直三棱柱
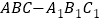 中,
中,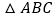 为正三角形,点
为正三角形,点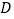 在棱
在棱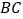 上,且
上,且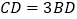 ,点
,点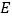 ,
,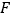 分别为棱
分别为棱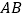 ,
,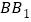 的中点.
的中点.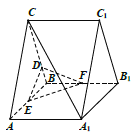
(1)证明:
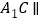 平面
平面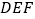 ;
;(2)若
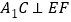 ,求直线
,求直线 与平面
与平面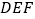 所成的角的正弦值.
所成的角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某技术公司开发的某种产品中随机抽取200件,测量这些产品的一项质量指标值(记为
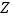 ),由测量结果得到如下频率分布直方图:
),由测量结果得到如下频率分布直方图: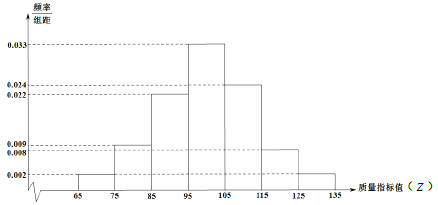
公司规定:当
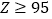 时,产品为正品;当
时,产品为正品;当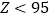 时,产品为次品,公司每生产一件这种产品,若是正品,则盈利90元;若是次品,则亏损30元,记
时,产品为次品,公司每生产一件这种产品,若是正品,则盈利90元;若是次品,则亏损30元,记 的分布列和数学期望;
的分布列和数学期望;由频率分布直方图可以认为,
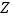 服从正态分布
服从正态分布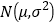 ,其中
,其中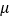 近似为样本平均数
近似为样本平均数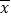 ,
,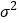 近似为样本方差
近似为样本方差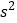 (同一组中的数据用该区间的中点值作代表)
(同一组中的数据用该区间的中点值作代表)①利用该正态分布,求
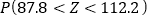 ;
;②某客户从该公司购买了500件这种产品,记
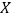 表示这500件产品中该项质量指标值位于区间
表示这500件产品中该项质量指标值位于区间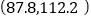 的产品件数,利用①的结果,求
的产品件数,利用①的结果,求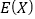 .
.附:
 ,
,若
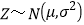 ,则
,则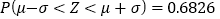 ,
,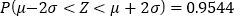 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设点
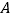 为圆
为圆 上的动点,点
上的动点,点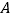 在
在 轴上的投影为
轴上的投影为 ,动点
,动点 满足
满足 ,动点
,动点 的轨迹为
的轨迹为 .
.(1)求
 的方程;
的方程;(2)设
 与
与 轴正半轴的交点为
轴正半轴的交点为 ,过点
,过点 的直线
的直线 的斜率为
的斜率为 ,
, 与
与 交于另一点为
交于另一点为 .若以点
.若以点 为圆心,以线段
为圆心,以线段 长为半径的圆与
长为半径的圆与 有4个公共点,求
有4个公共点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
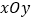 中,以坐标原点为极点,
中,以坐标原点为极点,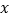 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为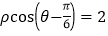 ,已知点
,已知点 为曲线
为曲线 上的动点,点
上的动点,点 在线段
在线段 上,且满足
上,且满足 ,动点
,动点 的轨迹为
的轨迹为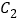 .
.(1)求
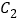 的直角坐标方程;
的直角坐标方程;(2)设点
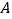 的极坐标为
的极坐标为 ,点
,点 在曲线
在曲线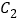 上,求
上,求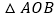 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在
 ,
, ,
, ,
, ,
, ,
, (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
(1)现按分层抽样从质量为
 ,
, 的芒果中随机抽取
的芒果中随机抽取 个,再从这
个,再从这 个中随机抽取
个中随机抽取 个,记随机变量
个,记随机变量 表示质量在
表示质量在 内的芒果个数,求
内的芒果个数,求 的分布列及数学期望.
的分布列及数学期望.(2)以各组数据的中间数代表这组数据的平均值,将频率视为概率,某经销商来收购芒果,该种植园中还未摘下的芒果大约还有
 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:A:所以芒果以
 元/千克收购;
元/千克收购;B:对质量低于
 克的芒果以
克的芒果以 元/个收购,高于或等于
元/个收购,高于或等于 克的以
克的以 元/个收购.
元/个收购.通过计算确定种植园选择哪种方案获利更多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直四棱柱
 中,底面
中,底面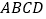 为等腰梯形,
为等腰梯形, .
.
(1)证明:
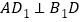 ;
;(2)设
 是线段
是线段 上的动点,是否存在这样的点
上的动点,是否存在这样的点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ,如果存在,求出
,如果存在,求出 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
相关试题

