【题目】设点![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,
,![]() 与
与![]() 交于另一点为
交于另一点为![]() .若以点
.若以点![]() 为圆心,以线段
为圆心,以线段![]() 长为半径的圆与
长为半径的圆与![]() 有4个公共点,求
有4个公共点,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用相关点法求出![]() 的方程;(2)由
的方程;(2)由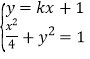 得
得![]() ,设
,设![]() ,
,![]() ,
,![]() ,则点
,则点![]() 的轨迹方程为
的轨迹方程为![]() ,
,
由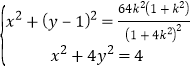 ,得
,得![]() ,(
,(![]() )(*)依题意得,(*)式关于
)(*)依题意得,(*)式关于![]() 的方程在
的方程在![]() 有两个不同的实数解,利用二次函数有关知识即可求出
有两个不同的实数解,利用二次函数有关知识即可求出![]() 的取值范围.
的取值范围.
试题解析:
(1)设点![]() ,
,![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以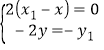 ,解得
,解得![]() ,
,
由于点![]() 在圆
在圆![]() 上,所以
上,所以![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)由(1)知,![]() 的方程为
的方程为![]() ,因为直线
,因为直线![]() .
.
由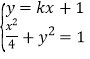 得
得![]() ,
,
设![]() ,
,![]() ,因此
,因此![]() ,
,![]() ,
,
![]() ,
,
则点![]() 的轨迹方程为
的轨迹方程为![]() ,
,
由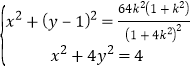 ,得
,得![]() ,(
,(![]() )(*)
)(*)
依题意得,(*)式关于![]() 的方程在
的方程在![]() 有两个不同的实数解,
有两个不同的实数解,
设![]() ,
,
因为函数![]() 的对称轴为
的对称轴为![]() ,
,
要使函数![]() 的图象在
的图象在![]() 与
与![]() 轴有两个不同的交点,
轴有两个不同的交点,
则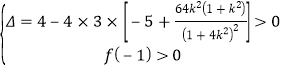 ,
,
整理得: ,即
,即![]() ,
,
所以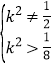 .
.
解得![]() ,
,
所以![]() 的取值范围为
的取值范围为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
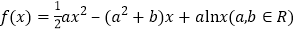 .
.(1)当
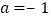 ,
,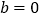 时,求函数
时,求函数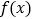 在
在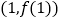 处的切线方程;
处的切线方程;(2)当
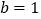 时,求函数
时,求函数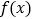 的单调区间;
的单调区间;(3)在(1)的条件下,证明:
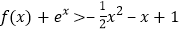 (其中
(其中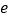 为自然对数的底数)
为自然对数的底数) -
科目: 来源: 题型:
查看答案和解析>>【题目】在直三棱柱
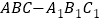 中,
中,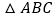 为正三角形,点
为正三角形,点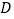 在棱
在棱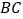 上,且
上,且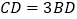 ,点
,点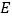 ,
,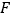 分别为棱
分别为棱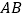 ,
,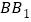 的中点.
的中点.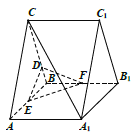
(1)证明:
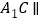 平面
平面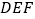 ;
;(2)若
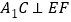 ,求直线
,求直线 与平面
与平面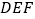 所成的角的正弦值.
所成的角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某技术公司开发的某种产品中随机抽取200件,测量这些产品的一项质量指标值(记为
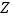 ),由测量结果得到如下频率分布直方图:
),由测量结果得到如下频率分布直方图: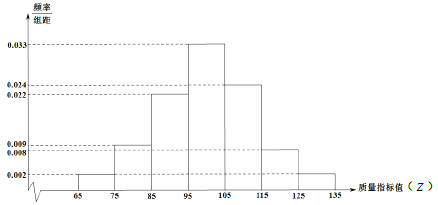
公司规定:当
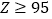 时,产品为正品;当
时,产品为正品;当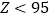 时,产品为次品,公司每生产一件这种产品,若是正品,则盈利90元;若是次品,则亏损30元,记
时,产品为次品,公司每生产一件这种产品,若是正品,则盈利90元;若是次品,则亏损30元,记 的分布列和数学期望;
的分布列和数学期望;由频率分布直方图可以认为,
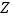 服从正态分布
服从正态分布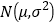 ,其中
,其中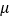 近似为样本平均数
近似为样本平均数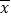 ,
,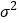 近似为样本方差
近似为样本方差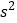 (同一组中的数据用该区间的中点值作代表)
(同一组中的数据用该区间的中点值作代表)①利用该正态分布,求
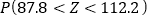 ;
;②某客户从该公司购买了500件这种产品,记
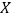 表示这500件产品中该项质量指标值位于区间
表示这500件产品中该项质量指标值位于区间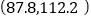 的产品件数,利用①的结果,求
的产品件数,利用①的结果,求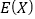 .
.附:
 ,
,若
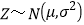 ,则
,则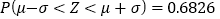 ,
,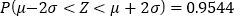 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求函数
 的零点个数;
的零点个数;(2)证明:当
 ,函数
,函数 有最小值,设
有最小值,设 的最小值为
的最小值为 ,求函数
,求函数 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
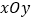 中,以坐标原点为极点,
中,以坐标原点为极点,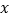 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为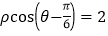 ,已知点
,已知点 为曲线
为曲线 上的动点,点
上的动点,点 在线段
在线段 上,且满足
上,且满足 ,动点
,动点 的轨迹为
的轨迹为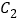 .
.(1)求
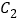 的直角坐标方程;
的直角坐标方程;(2)设点
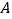 的极坐标为
的极坐标为 ,点
,点 在曲线
在曲线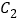 上,求
上,求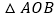 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在
 ,
, ,
, ,
, ,
, ,
, (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
(1)现按分层抽样从质量为
 ,
, 的芒果中随机抽取
的芒果中随机抽取 个,再从这
个,再从这 个中随机抽取
个中随机抽取 个,记随机变量
个,记随机变量 表示质量在
表示质量在 内的芒果个数,求
内的芒果个数,求 的分布列及数学期望.
的分布列及数学期望.(2)以各组数据的中间数代表这组数据的平均值,将频率视为概率,某经销商来收购芒果,该种植园中还未摘下的芒果大约还有
 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:A:所以芒果以
 元/千克收购;
元/千克收购;B:对质量低于
 克的芒果以
克的芒果以 元/个收购,高于或等于
元/个收购,高于或等于 克的以
克的以 元/个收购.
元/个收购.通过计算确定种植园选择哪种方案获利更多?
相关试题

