【题目】在直三棱柱![]() 中,
中,![]() 为正三角形,点
为正三角形,点![]() 在棱
在棱![]() 上,且
上,且![]() ,点
,点![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点.
的中点.
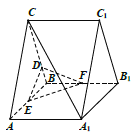
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接![]() ,
,![]() ,交于点
,交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,易证
,易证![]() ,从而得证;(2)以点
,从而得证;(2)以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立空间直角坐标系,平面
轴的正方向,建立空间直角坐标系,平面![]() 的法向量为
的法向量为![]() ,
,![]() ,利用公式即可得到直线
,利用公式即可得到直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
试题解析:
(1)证明:如图,连接![]() ,
,![]() ,交于点
,交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
因为![]() 为矩形,所以
为矩形,所以![]() 为线段
为线段![]() 的中点,
的中点,
因为点![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点,
的中点,
所以点![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)由(1)知,![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 为正三角形,且点
为正三角形,且点![]() 为棱
为棱![]() 的中点,
的中点,
所以![]() ,
,
故以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
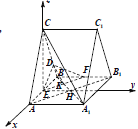
轴,![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() ,设
,设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,解得
,解得![]() .
.
所以![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则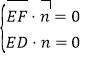 ,所以
,所以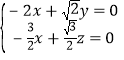 ,
,
取![]() ,则
,则![]() ,
,
又因为![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以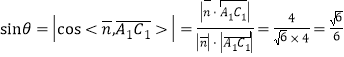 ,
,
所以直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】11月11日有2000名网购者在某购物网站进行网购消费(金额不超过1000元),其中女性1100名,男性900名.该购物网站为优化营销策略,根据性别采用分层抽样的方法从这2000名网购者中抽取200名进行分析,如表.(消费金额单位:元)

(1)计算
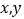 的值,在抽出的200名且消费金额在
的值,在抽出的200名且消费金额在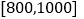 的网购者中随机抽出2名发放网购红包,求选出的2人均为女性的概率;
的网购者中随机抽出2名发放网购红包,求选出的2人均为女性的概率;(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上数据列
 列联表,并回答能否有
列联表,并回答能否有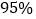 的把握认为“是否为网购达人与性别有关?”附:
的把握认为“是否为网购达人与性别有关?”附: ,
,

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
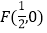 为抛物线
为抛物线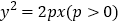 的焦点,点
的焦点,点 为其上一点,
为其上一点,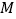 与
与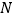 关于
关于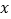 轴对称,直线
轴对称,直线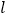 与抛物线交于异于
与抛物线交于异于 的
的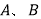 两点,
两点,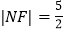 ,
,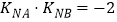 .
.(1)求抛物线的标准方程和
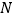 点的坐标;
点的坐标;(2)判断是否存在这样的直线
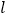 ,使得
,使得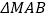 的面积最小.若存在,求出直线
的面积最小.若存在,求出直线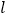 的方程和
的方程和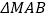 面积的最小值;若不存在,请说明理由.
面积的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
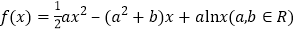 .
.(1)当
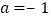 ,
,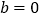 时,求函数
时,求函数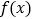 在
在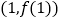 处的切线方程;
处的切线方程;(2)当
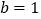 时,求函数
时,求函数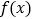 的单调区间;
的单调区间;(3)在(1)的条件下,证明:
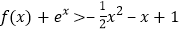 (其中
(其中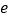 为自然对数的底数)
为自然对数的底数) -
科目: 来源: 题型:
查看答案和解析>>【题目】从某技术公司开发的某种产品中随机抽取200件,测量这些产品的一项质量指标值(记为
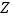 ),由测量结果得到如下频率分布直方图:
),由测量结果得到如下频率分布直方图: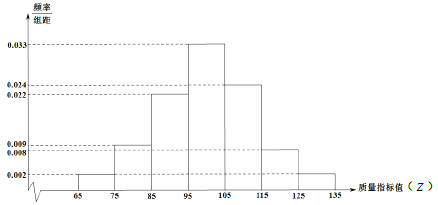
公司规定:当
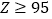 时,产品为正品;当
时,产品为正品;当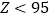 时,产品为次品,公司每生产一件这种产品,若是正品,则盈利90元;若是次品,则亏损30元,记
时,产品为次品,公司每生产一件这种产品,若是正品,则盈利90元;若是次品,则亏损30元,记 的分布列和数学期望;
的分布列和数学期望;由频率分布直方图可以认为,
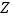 服从正态分布
服从正态分布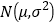 ,其中
,其中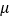 近似为样本平均数
近似为样本平均数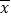 ,
,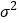 近似为样本方差
近似为样本方差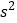 (同一组中的数据用该区间的中点值作代表)
(同一组中的数据用该区间的中点值作代表)①利用该正态分布,求
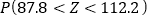 ;
;②某客户从该公司购买了500件这种产品,记
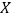 表示这500件产品中该项质量指标值位于区间
表示这500件产品中该项质量指标值位于区间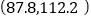 的产品件数,利用①的结果,求
的产品件数,利用①的结果,求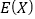 .
.附:
 ,
,若
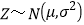 ,则
,则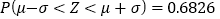 ,
,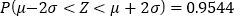 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设点
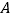 为圆
为圆 上的动点,点
上的动点,点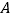 在
在 轴上的投影为
轴上的投影为 ,动点
,动点 满足
满足 ,动点
,动点 的轨迹为
的轨迹为 .
.(1)求
 的方程;
的方程;(2)设
 与
与 轴正半轴的交点为
轴正半轴的交点为 ,过点
,过点 的直线
的直线 的斜率为
的斜率为 ,
, 与
与 交于另一点为
交于另一点为 .若以点
.若以点 为圆心,以线段
为圆心,以线段 长为半径的圆与
长为半径的圆与 有4个公共点,求
有4个公共点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求函数
 的零点个数;
的零点个数;(2)证明:当
 ,函数
,函数 有最小值,设
有最小值,设 的最小值为
的最小值为 ,求函数
,求函数 的值域.
的值域.
相关试题

